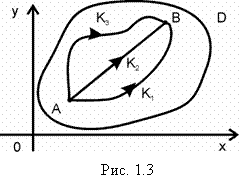
Пусть Х = Х(х, у),  Y = Y(x, y) – непрерывные функции в области D (рис. 1.3). Пусть А(х₁, у₁) и В(х₂, у₂) две произвольные точки области D и пути К₁, К₂ и К₃, соединяющие эти точки (условимся считать, что М₁ – начало, а М₂ – конец пути) (рис. 1.3).

Если взять криволинейные интегралы второго рода по этим путям и получится, что результаты равны, то говорят, что криволинейный интеграл второго рода  не зависит от формы пути интегрирования в данной области D. В таком случае нет необходимости указывать путь интегрирования, а достаточно указать начало и конец пути и употребляется запись:

.       (1.22)

Справедлива теорема: если в области D подынтегральное выражение Xdx + Ydy является полным дифференциалом некоторой функции U  =U(x, y), т.е.

, при ,                                                (1.23)

то криволинейный интеграл (I.4.1.) не зависит от пути интегрирования в области D.

Доказательство. Пусть x = x(t),  y = y(t),  z = z(t)   – произвольный путь К в D, соединяющий А и В, причём

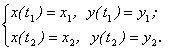                                                  (1.24)

Из формулы (1.23) имеем:

                                                  (1.25)

Отсюда

.                  (1.26)

Используя (1.24), будем иметь:

.                            (1.27)

Вывод: Значения интеграла J одно и тоже при любом выборе функций x(t),  y(t) и, следовательно, интеграл J  не зависит от формы пути, соединяющего точки А(х₁, у₁) и В(х₂, у₂).

В этом случае приходят к формуле Ньютона-Лейбница для криволинейного интеграла второго рода:

                                      (1.28)

Следствие: если подынтегральное выражение  Xdx + Ydy есть полный дифференциал и путь интегрирования К замкнутый, то

                                                           (1.29)

Замечание. Условие полного дифференциала для выражения Xdx + Ydy имеет вид:

                                                               (1.30)

Пример 1

Вычислить .

Решение. Так как ydx + xdy – есть полный дифференциал некоторой функции d, ибо условие (1.30) выполняется, то

Пример 2

Вычислить , К – окружность радиуса R с центром в начале координат.

Решение. Полный дифференциал функции U(x,y) = arctg (проверьте). Следовательно, интеграл согласно (1.28) должен быть равен нулю. Непосредственно вычислим его:

Причина состоит в том, что функции

  и 

теряют смысл в точке (0; 0), что находится в области, ограниченной замкнутым контуром К, и не являются непрерывными.

Замечание. Полученные результаты полностью распространяются на случай трехмерного пространства:

если функции X(x, y, z), Y(x, y, z) и Z(x, y, z), , , , ,  и  – непрерывны в замкнутой области D, то выполнение во всех точках области D условий:

                                             (1.31)

необходимо и достаточно для того, чтобы криволинейный интеграл  был равен нулю.

Эта теорема будет доказана позже.