Как известно из интегрального исчисления функции одной переменной [4] определенный интеграл дает величину площади криволинейной трапеции.

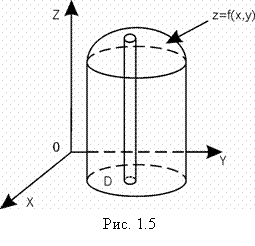Выясним геометрический смысл двойного интеграла. Предположим, что функция f(P) = f(x,y) ≥ z и рассмотрим в пространстве тело Т, ограниченное снизу областью D, сверху поверхностью z = f(x, y), а с боков цилиндрической поверхностью с образующей параллельной оси Оz (рис. 1.5). Такое тело называют цилиндрическим брусом.

Ставим задачу: найти объём цилиндрического бруса Т. Следуя схеме нахождения определенного интеграла (двойного), приходим к интегральной сумме, которая приближенно дает объём:

Чтобы получить точное значение V следует перейти к пределу при :

.          (1.41)

В этом заключается геометрический смысл  двойного интеграла.

Замечание:

а) Если L – кривая, лежащая в плоскости xОy, то геометрический смысл криволинейного интеграла , считая  дает  площадь куска цилиндрической поверхности с направляющей L и образующий, параллельной oz, срезанного сверху поверхностью  z = f(x, y).

б) Поверхностный и тройной интегралы не имеют при произвольной интегрируемой функции f(P) простого геометрического смысла (что не мешает использовать их для нахождения геометрических величин).

в) Основные свойства полученных типов интегралов доказываются аналогично свойствам определенного интеграла. Отметим свойство, важное для приложений интегралов к вычислению геометрических величин, а именно: если функция  на фигуре, то интеграл от неё даёт меру фигуры:

1)   – длину отрезка [a,b];                                                               (1.42)

2)  – длину линии L;                                                                                         (1.43)

3)  – площадь области D;                                                                               (1.44)

4)  – площадь поверхности S;                                                                        (1.45)

5)  – объем тела V.                                                                                         (1.46)