Пусть функции ![]() и
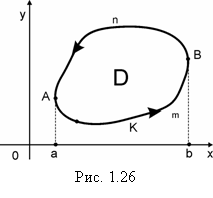
и ![]() непрерывно дифференцируемы в области D (рис. 1.26), ограниченной замкнутой кривой К, тогда имеет место формула:
непрерывно дифференцируемы в области D (рис. 1.26), ограниченной замкнутой кривой К, тогда имеет место формула:
![]() (1.70)
(1.70)
 Формулу (1.70) называется формулой Грина, она играет фундаментальную роль в векторном анализе.
Формулу (1.70) называется формулой Грина, она играет фундаментальную роль в векторном анализе.
Доказательство. Примем х за параметр. Тогда
 (1.71)
(1.71)
Аналогично находим:
![]() (1.72)
(1.72)
Складывая почленно (1.70) и (1.72), получим формулу Грина:
![]()
Формула Грина связывает криволинейный интеграл по координатам с двойным интегралом по области, ограниченной замкнутым контуром К.
Пример 1
Написать и проверить формулу Грина для интеграла ![]() , где К:
, где К: ![]() , ограничивающая круг D.
, ограничивающая круг D.
Решение. Имеем: ![]() . По формуле (1.70) находим:
. По формуле (1.70) находим:
![]() (1.73)
(1.73)
Перейдя к полярным координатам, вычислим двойной интеграл в (1.73):
![]() (1.74)
(1.74)
Вычислим интеграл левой части (1.73), введя параметр t в уравнение окружности ![]() :
:
![]() (1.75)
(1.75)
отсюда видно, что требования задачи удовлетворяются. Тем самым мы вычислили криволинейный интеграл через двойной.
Замечание. С помощью формулы Грина можно вычислять площади плоских фигур. Таких формул приведем три:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Задачи для упражнений
1) Вывести формулы, записанные в замечании.
2) Написать и проверить формулу Грина для ![]() , где К – контур треугольника со сторонами x = 0, y = 0, x + y = a.
, где К – контур треугольника со сторонами x = 0, y = 0, x + y = a.
3) Применяя формулу Грина, вычислить криволинейный интеграл ![]() , где K:
, где K: ![]() . Ответ:
. Ответ: ![]() .
.
4) Показать, что ![]() по любому замкнутому контуру К равен 0.
по любому замкнутому контуру К равен 0.
5) Вывести одну из формул, для вычисления площади с помощью криволинейного интеграла второго рода.