1.4.5. Теорема Стокса | Электронная библиотека

Естественные науки / Специальные главы высшей математики / 1.4.5. Теорема Стокса

Теорема Стокса является одной из важных теорем векторного анализа. Она устанавливает связь между циркуляцией поля по любому контуру L и потоком вихря поля через любую поверхность, натянутую на контур L.

Теорема. Циркуляция поля по контуру L равна потоку вихря поля через любую поверхность S, лежащую в векторном поле и имеющую своей границей контур L:

(1.110)

При этом предполагается, что на поверхности S все частные производные первого порядка от функции – непрерывны. Нормаль выбрана к поверхности S так, что бы циркуляция рассматривалась в положительном направлении.

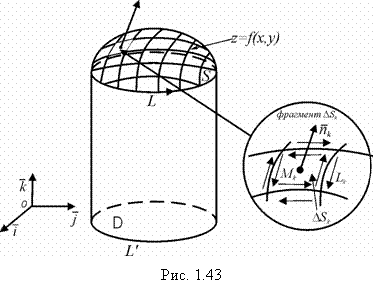
Доказательство. Пусть на контур L натянута гладкая произвольная поверхность (рис. 1.43).Её уравнение обозначим функцией . Разобьем поверхность S на n элементарных площадок (k = 1, 2, ….n) ограниченных замкнутыми линиями . В каждой из них возьмём точкуи определим проекции вихря в на направление :

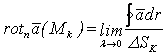По определению предела переменной известно, что

где S – площадь поверхности S.

Умножив наи просуммировав, получим:

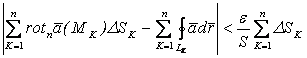В правой части последнего неравенства , сократив эту часть на S, получим . В сумме 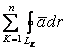интегралы по всем линиям, лежащим в области, ограниченной контуром L, попарно уничтожаются, так как интегрирование по ним происходит в двух взаимно противоположенных направлениях (рис. 1.4).

Поэтому

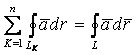Учитывая это, получим:

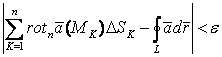Отсюда, следуя определению предела переменной, имеем: 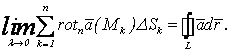Однако предел левой части – предел интегральной суммы для поверхностного интеграла второго рода, поэтому

Замечание 1. Дивергенция и вихрь векторного поля являются локальными характеристиками поля, в то время как теоремы Остроградского и Стокса являются интегральными характеристиками векторного поля.

Пример

Вычислить циркуляцию поля вектора по линии пересечения поверхности с координатными плоскостями в положительном направлении (непосредственно и при помощи теоремы Стокса).

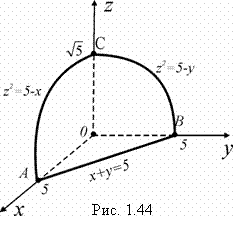
Решение. Непосредственное вычисление заключается в том, что применяют формулу (1.106). Обычно используют метод «сечений» построения поверхности (рис. 1.44), полагая последовательно x = 0, y = 0, z =0.

На рис. 1.44 указанно направление положительного обхода контура ABCA. Согласно (1.106) и свойству аддитивности имеем:

Вычислим каждый интеграл в отдельности и сложим все полученные результаты, получим циркуляцию Г по замкнутому контуру. Итак,

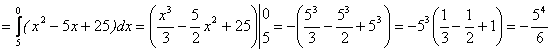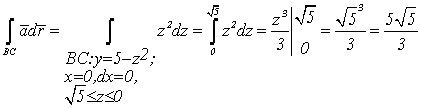
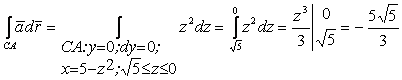Следовательно, – это говорит о том, что контур вращается в направлении, противоположенном выбранному.

Найдем Г по теореме Стокса, а именно, используя формулу (1.110). Вычислим вихрь поля:

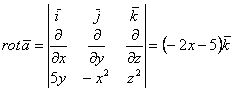
В качестве поверхности S в формуле (1.110) возьмём боковую поверхность пирамиды, опирающуюся на контур ABCA.

Тогда , на грани OAC вектор , поэтому и ; на грани OAB вектор , поэтому

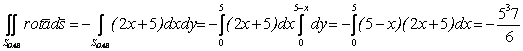На грани OCB вектор , поэтому и .

В итоге получим: .

Задачи для упражнений

1) Найти от по направлению от точки М₀(1; 1; 1) к точке (2; 2; 2)

Ответ: .

2) Найти от в точке М₀(1; 1; 1) по направлению вектора , образующего с координатными осями Ox и Oy соответственно углы , а с Oz угол . Ответ: .

3) Найти , если в точке .

Ответ: .

4) Найти: . Ответ: .

5) Найти: . Ответ: .

1) Найти градиент скалярного поля в точке .

Ответ: .

7) Вычислить с помощью градиента производную поля в точке (2; 3; 6) по направлению радиуса-вектора этой точки. Ответ: .

8) Найти векторные линии поля 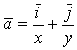. Ответ: .

9) Найти: векторные линии поля 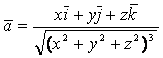. Ответ: .

10) Найти: векторные линии поля . Ответ: .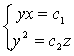

11) Найти поток поля через поверхность прямого конуса радиуса R и высоты H, вершина которого находится в начале координат.

Ответ: .

12) Найти поток поля вектора через часть плоскости , лежащую в первом октанте. Ответ: .

13) Найти поток векторного поля через поверхность пирамиды с вершиной в точке и основанием OAB, где : а) непосредственно; б) по теореме Остроградского.

Ответ: П = 0.

14) Найти поток поля вектора через поверхность пирамиды, ограниченной плоскостями непосредственно и по теореме Остроградского. Ответ:

15) Вычислить поток по теореме Остроградского, если поле через полную поверхность цилиндра: .

Ответ: .

16) Найти , где . Ответ: .

17) Найти , если в точке .

Ответ: 6.

18) Найти , если 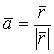. Ответ: .

19) Найти поток поля , образованный плоскостями х = 0, y= 0; z = 0 через замкнутую поверхность, параболоида , лежащую в первом октане. Воспользоваться цилиндрическими координатами. Ответ: .