В теории поля и ее приложениях рассматриваются так называемые потенциальные поля.
Определение. Поле вектора ![]() называется потенциальным, если вектор
называется потенциальным, если вектор ![]() является градиентом некоторой скалярной функции
является градиентом некоторой скалярной функции ![]() :
:
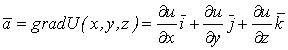 . (1.111)
. (1.111)
(поле в этом случаи называют также безвихревым или градиентным).
Функция ![]() называется потенциальной функцией поля. Часто говорят, что скалярная функция
называется потенциальной функцией поля. Часто говорят, что скалярная функция ![]() называется скалярным потенциалом поля.
называется скалярным потенциалом поля.
 Замечание. В литературе дается определение потенциального поля и так, что
Замечание. В литературе дается определение потенциального поля и так, что ![]() . Знак «минус» перед
. Знак «минус» перед ![]() берётся для удобства. Это не имеет принципиального значения. При изучении понятия потенциального векторного поля надо уточнять, каким образом вводится понятие потенциального поля. В частности, для электрического поля:
берётся для удобства. Это не имеет принципиального значения. При изучении понятия потенциального векторного поля надо уточнять, каким образом вводится понятие потенциального поля. В частности, для электрического поля:
![]()
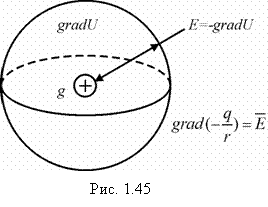
Знак «минус» перед ![]() имеет здесь физический смысл, он означает, что в направлении вектора напряженности
имеет здесь физический смысл, он означает, что в направлении вектора напряженности ![]() электрический потенциал убывает (рис. 1.45).
электрический потенциал убывает (рис. 1.45).
Если ![]() – потенциальная функция вектора
– потенциальная функция вектора ![]() , то
, то ![]() , где
, где ![]() , тоже будет потенциальной, так как
, тоже будет потенциальной, так как ![]() .
.
Поле не всякого вектора является потенциальным. Возникает задача: по какому признаку установить, будет ли поле ![]() потенциальным? Следующая теорема дает утвердительный ответ и, что важно, приводит к методу нахождения этой функции.
потенциальным? Следующая теорема дает утвердительный ответ и, что важно, приводит к методу нахождения этой функции.
Теорема: Для того чтобы поле ![]() было потенциальным, необходимо и достаточно, чтобы вихрь этого поля равнялся нулю:
было потенциальным, необходимо и достаточно, чтобы вихрь этого поля равнялся нулю:
![]() .
.
Доказательство. Необходимость. Дано, что ![]() — потенциальное поле. Тогда, согласно определению (1.111),
— потенциальное поле. Тогда, согласно определению (1.111), ![]() , т.е.
, т.е.
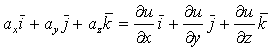 .
.
Отсюда заключаем, что
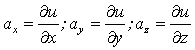 .
.
Найдем вихрь поля:
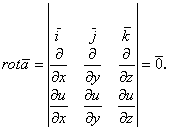
Что и требовалось доказать.
Достаточность. Дано, что ![]() , т.е.
, т.е.
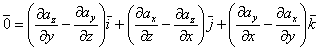
Отсюда
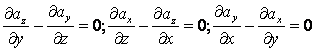 (1.112)
(1.112)
Это есть условие полного дифференциала функции ![]() [6], т.е.
[6], т.е.
![]() (1.113)
(1.113)
Следовательно, искомая функция (потенциальная) может быть найдена так:
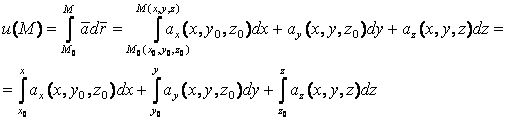 (1.114)
(1.114)
Полный дифференциал функции ![]() :
:
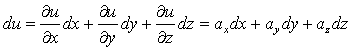 , т.е.
, т.е.
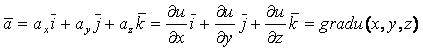 ,
,
Отсюда поле вектора ![]() — потенциально.
— потенциально.
Замечание 1. Потенциальное поле обладает рядом особенностей:
а) Потенциальное поле характеризуется лишь одной скалярной функцией ![]() , в то время как любое векторное поле
, в то время как любое векторное поле ![]() определяется тройкой скалярных функций
определяется тройкой скалярных функций ![]() .
.
б) Циркуляция в потенциальном поле по любому контуру равна нулю. Это следует из теоремы Стокса:
![]() , так как
, так как ![]() .
.
в) В потенциальном поле криволинейный интеграл не зависит от формы пути интегрирования (доказано при рассмотрении условия независимости криволинейного интеграла от формы пути интегрирования).
Методическое руководство
 При нахождении потенциальной функции в качестве начальной точки
При нахождении потенциальной функции в качестве начальной точки ![]() берут начало координат, если эта точка принадлежит области, в которой ищется потенциальная функция – это упрощает вычисления; согласно замечанию криволинейный интеграл не зависит от формы пути интегрирования, поэтому удобно брать путь – ломаную (см. рис. 1.46), тогда:
берут начало координат, если эта точка принадлежит области, в которой ищется потенциальная функция – это упрощает вычисления; согласно замечанию криволинейный интеграл не зависит от формы пути интегрирования, поэтому удобно брать путь – ломаную (см. рис. 1.46), тогда:
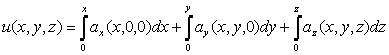 (1.115)
(1.115)
Если найти ![]() , то должны получить вектор
, то должны получить вектор ![]() . Это Можно считать проверкой.
. Это Можно считать проверкой.
Итог: Криволинейный интеграл потенциального поля на пути ![]() равен разности потенциальной функции в конечной и начальной точках этого пути:
равен разности потенциальной функции в конечной и начальной точках этого пути:
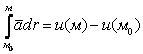 , (1.116)
, (1.116)
другими словами, для потенциального поля ![]() имеет место формула Ньютона-Лейбница. Она позволит по известной потенциальной функции найти криволинейный интеграл второго рода (роль первообразной здесь играет потенциальная функция
имеет место формула Ньютона-Лейбница. Она позволит по известной потенциальной функции найти криволинейный интеграл второго рода (роль первообразной здесь играет потенциальная функция ![]() поля
поля ![]() ).
).
Пример
Проверить, будет ли поле вектора ![]() потенциальным? В случаи его потенциальности найти потенциальную функцию.
потенциальным? В случаи его потенциальности найти потенциальную функцию.
Решение. Найдем вихрь этого поля:
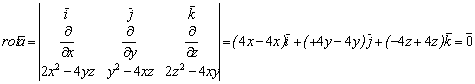
Согласно признаку потенциальности поле – потенциальное. Следовательно, существует потенциальная функция, которую найдем, используя формулу (1.115):
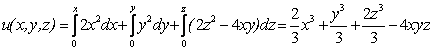 ,
,
то есть
![]() .
.
В общем случае, если ![]() — произвольная точка, то
— произвольная точка, то
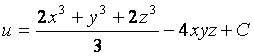 .
.
Проверка:
![]() .
.
Задачи для упражнений
1) Найти потенциал поля ![]() .
.
Ответ: ![]() .
.
2) Будет ли поле вектора ![]() потенциальным? В случае потенциальности найти u(х, y, z)
потенциальным? В случае потенциальности найти u(х, y, z)
Ответ: ![]() .
.
3) Условия прежние:
а) ![]() Ответ:
Ответ: ![]()
б) ![]() Ответ:
Ответ: ![]()