Множество L называется линейным пространством , а его элементы — векторами (будем обозначать их с чертой сверху), если:1) определена операция сложения, которая 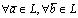 ставит в соответствие элемент
ставит в соответствие элемент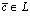 , называемый суммой, который обозначается
, называемый суммой, который обозначается 2) определена операция умножения на число, которая
2) определена операция умножения на число, которая 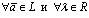 ставит в соответствие элемент
ставит в соответствие элемент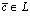 , называемый произведением вектора
, называемый произведением вектора 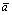 на число
на число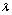 , который обозначается
, который обозначается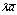 ;3)
;3)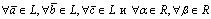 выполняются следующие аксиомы:
выполняются следующие аксиомы:
1°.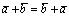 ;2о.
;2о.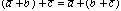 ; 3°. существует единственный вектор
; 3°. существует единственный вектор 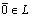 такой, что
такой, что 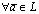 справедливо равенство:
справедливо равенство: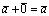 ;4°.
;4°.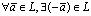 такой, что ;
такой, что ;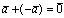 ;5°.
;5°.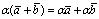 ;6°.
;6°.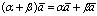 ;7°.
;7°.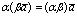 ;8°.
;8°.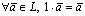 .
.