Для определения количества теплоты, проходящей за время  через изотермическую поверхность  твердого тела конечных размеров, необходимо проинтегрировать уравнение, отражающее закон Фурье, по и , т.е. необходимо знать температурное поле внутри рассматриваемого тела и знать, как оно изменяется с течением времени.

Для решения этой задачи выводится дифференциальное уравнение теплопроводности при следующих допущениях: тело однородное, физические параметры его постоянны. В соответствии с законом сохранения энергии количество теплоты (), введенное в элементарный объем за время  путем теплопроводности, плюс количество теплоты, выделяемое внутренними источниками , должно быть равно изменению внутренней энергии вещества ():

Для определения членов этого уравнения в декартовой системе координат выделим в теле элементарный параллелепипед со сторонами  (рис. 10.4). Подводимую теплоту обозначим через , а отводимую – .

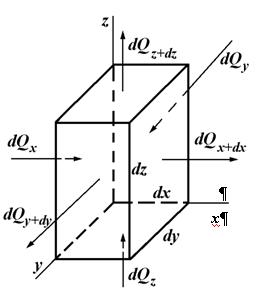
Рис. 10.4. Схема для вывода дифференциального уравнения энергии

Тогда для грани  из закона Фурье найдем:

;

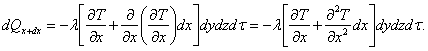
Разность величин представляет собой количество теплоты, остающейся в параллелепипеде:

.

Аналогичные зависимости получаются для двух других граней:

;       .

Тогда общее количество теплоты, оставшееся в теле, равно:

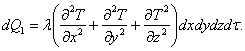
Если обозначить через  удельную теплопроизводительность внутренних источников тепла, то можно записать:

.

Изменение внутренней энергии тела за время  составляет:

.

Таким образом, окончательно получим:

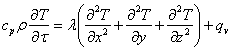
или

.

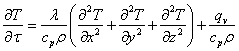Введем обозначение:  – коэффициент температуропроводности, который характеризует степень нестационарности режима. Подставим его в последнее уравнение, получим:

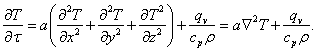
Таким образом, получено уравнение, связывающее временное и пространственное изменения температуры в любой точке тела.