Изучая курс высшей математики, мы неоднократно пользовались некоторыми понятиями теории функций комплексного переменного (ТФКП). Сделаем попытку более подробно изложить основы этой теории, которая имеет важную роль в математике и ее многочисленных приложениях.
Понятие числа – одно из основных в математике и имеет многовековую историю. Число возникло не в результате свободного творчества человека, а было создано для удовлетворения практических потребностей. В процессе развития практической деятельности людей понятие числа изменялось и совершенствовалось, и в итоге были получены вещественные числа (числа рациональные и иррациональные, положительные и отрицательные). Геометрически вещественные числа изображаются точками числовой оси – прямой, на которой указано положительное направление, масштаб и начало отсчета.
Однако не успело закрепиться новое расширенное понятие числа, как в процессе дальнейшего развития математики возникла нужда в расширении множества действительных чисел. Ввели так называемые мнимые числа. Новую единицу обозначили буквой i, понимая величину ![]() , или i2 = –1 (буква i – первая бува слова imaginarius, что означает «мнимый»). После введения этой единицы стало возможным извлечение квадратного корня из отрицательного числа, что в множестве вещественных чисел невозможно.
, или i2 = –1 (буква i – первая бува слова imaginarius, что означает «мнимый»). После введения этой единицы стало возможным извлечение квадратного корня из отрицательного числа, что в множестве вещественных чисел невозможно.
По исторической традиции число i назвали мнимой единицей, а число ib – чисто мнимыми числами.
Число вида a+ib получило название комплексного числа, в котором различают действительную часть а и мнимую часть b.
С расширением понятия числа, целый ряд вопросов, которые в области действительного переменного не могли быть решены, получили простое и естественное объяснение в области комплексного переменного.
Обозначим комплексное число ![]() одной буквой z:
одной буквой z:
![]() (2.1)
(2.1)
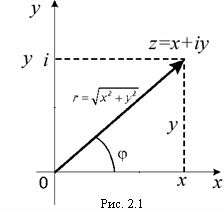
Этой же буквой обозначим точку на плоскости xОy, изображающую собой это число z = x + iy (рис. 2.1). Числа х и у называют, соответственно, действительной и мнимой частями числа z и обозначают символами:
x = Re z (2.2)
(от латинского слова realis – действительный),
y = Jm z (2.3)
(от латинского слова imaginarius – мнимый).
Числа x и y являются также координатами точки в комплексной плоскости x и y. Множество всех действительных чисел изображается осью абсцисс, называемой поэтому действительной осью; множество всех чисто мнимых чисел лежит на оси ординат, называемой мнимой осью. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью или плоскостью z (будем обозначать ![]() множество
множество
всех конечных чисел z и z без кружка – расширенную комплексную плоскость, рассматривая и z = ¥ – называемую бесконечно удаленной точкой).
Комплексное число z = x + iy можно трактовать как вектор OZ исходящий из начала координат. Число z = 0, если x = 0 и y = 0. Вообще: два комплексных числа z1 и z2 равны тогда и только тогда, когда Rez1 = Rez2 и Jmz1 = Jmz2. То есть понятие о равенстве двух комплексных чисел вытекает из их геометрической интерпретации (две точки на плоскости совпадают только в том случае, если эти точки имеют одинаковые координаты по осям).
Знаками неравенства комплексные числа соединять нельзя.
Вектор z = x + iy можно определить не только координатами х и у; его можно определить однозначно и полярными координатами: длиной вектора r = |z| и углом j, который вектор z образует с положительным направлением оси Ох (см. рис. 2.1).
Из DОхz имеем:
х = r cos j; у = r sin j; (2.4)
r = + ![]() ; tg j =
; tg j = ![]() ; j = arctg
; j = arctg ![]() . (2.5)
. (2.5)
Положительное число r = |z| называется модулем, а угол j аргументом комплексного числа z = x+iy и обозначается:
j = Arg z (z ¹ 0). (2.6)
Отметим, что при данных х и у модуль числа z определяется единственным образом, а аргумент j определяется лишь с точностью до слагаемого, кратного 2p, так как вектор z совместится сам с собой, если его повернуть на любое число полных оборотов в ту или другую сторону вокруг точки О.
Вывод: если два комплексных числа равны, то модули их равны, а аргументы могут отличаться слагаемым 2kp (k = 0, ± 1, …).
Используя (2.4) число z = x + iy можем представить в форме:
z = r (cos j + i sin j). (2.7)
Эта форма комплексного числа называется тригонометрической, а форма (2.1) называется алгебраической. Отметим, что аргумент числа z=0 не определяется, а то значение аргумента j0, которое удовлетворяет условию –p < j0 £ p, называется главным значением аргумента и обозначается: arg z. Итак,
Arg z = arg z + 2kp (k = 0, ± 1, ± 2, …). (2.8)
Для главного значения аргумента верны соотношения:
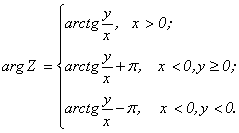 (2.9)
(2.9)
Например, arg1 = 0, Arg1 = 2kp;
arg i = ![]() , Arg i =
, Arg i = ![]() + 2kp;
+ 2kp;
arg(i+1) = ![]() , Arg(i+1) =
, Arg(i+1) = ![]() + 2kp;
+ 2kp;
arg(i-1) = ![]() , Arg(i-1) =
, Arg(i-1) = ![]() + 2kp;
+ 2kp;
arg (-1) = ![]() , Arg(-1) = (2k+1)
, Arg(-1) = (2k+1) ![]() .
.