В достаточно общем случае изучаемый технический объект количественно можно охарактеризовать векторами

,  и

внешних, внутренних и выходных параметров соответственно. Одни и те же физические, механические или информационные характеристики ТО в моделях различного уровня и содержания могут выполнять роль, как внешних или внутренних, так и выходных параметров.

Для большинства случаев абстрактная модель системы произвольной природы может быть представлена с помощью схемы (рис. 2.1), Система не существует сама по себе, а выделяется из окружающей среды по какому-либо системообразующему признаку, в качестве которого чаще всего выступает цель системы. Взаимодействие системы с внешней средой осуществляется через вход и выход системы (множество входных и выходных параметров).

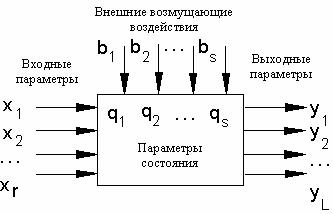
Рис. 2.1 Модель произвольного объекта

Под входными параметрами системы понимается комплекс параметров внешней среды (в том числе выходные параметры систем, внешних по отношению к рассматриваемой, например, систем управления), оказывающих значительное влияние

на состояние и значение выходных параметров рассматриваемой системы и поддающихся учету и анализу средствами, имеющимися в распоряжении исследователя.

Выходные параметры – это комплекс параметров системы, оказывающих непосредственное влияние на состояние внешней среды и значимых с точки зрения цели исследования.

Важной особенностью функционирования сложных систем является принципиальная неопределенность истинного состояния внешней среды в каждый момент времени. Природа этой неопределенности связана с наличием ряда причин, важнейшие из которых обусловлены следующими факторами:

1) о некоторых, возможно, непосредственно влияющих на поведение системы параметрах внешней среды (то есть параметрах, которые следовало бы отнести к категории «входных»), исследователь часто не знает, и, следовательно, не может их учитывать;

2) некоторые параметры внешней среды не могут быть измерены в силу технической неприспособленности информационных средств;

3) численные значения учитываемых параметров оцениваются с ошибками измерений, определяемыми, с одной стороны, внутренними шумами измерительных устройств, а с другой – внешними помехами.

Воздействие на систему подобных неучтенных факторов компенсируется введением в модель дополнительных связей – внешних возмущающих воздействий или «шумов».

Система может находиться в различных состояниях. Состояние любой системы в определенный момент времени можно с определенной точностью охарактеризовать совокупностью значений параметров состояния q.

Таким образом, система характеризуется тремя группами переменных:

1) входными переменными, которые генерируются системами, внешними относительно исследуемой

;

2) выходными переменными, определяющие воздействие исследуемой системы на окружающую среду

;

3) параметрами состояния (внутренними параметрами), характеризующими динамическое поведение исследуемой системы

.

При исследовании большинства систем все три группы введенных величин предполагаются функциями времени.

При создании ТО значения выходных параметров или диапазоны их возможного изменения оговаривают в техническом задании на разработку ТО, тогда как внешние параметры характеризуют условия его функционирования.

В сравнительно простом случае математическая модель ТО может представлять собой соотношение:

;    ;   ;   ,   (2.1)

где f – векторная функция векторного аргумента. Модель в виде соотношения (2.1) позволяет легко вычислять выходные параметры по задаваемым значениям внешних и внутренних параметров, т.е. решать так называемую прямую задачу.

В инженерной практике решение прямой задачи часто называют поверочным расчетом. При создании ТО возникает необходимость решать более сложную так называемую обратную задачу: по обусловленным техническим заданием на проектирование ТО значениям внешних и выходных параметров находить его внутренние параметры. В инженерной практике решению обратной задачи соответствует проектировочный расчет, часто имеющий целью оптимизацию внутренних параметров по некоторому критерию оптимальности. Однако при построении ММ ТО функция f в соотношении (2.1) обычно заранее не известна и ее предстоит установить. Это наиболее сложная так называемая задача идентификации ММ.

Задача идентификации может быть решена путем математической обработки информации о ряде таких состояний ТО, для каждого из которых известны (например, измерены экспериментально) значения выходных, внутренних и внешних параметров. Один из таких способов связан с применением регрессионного анализа. Если информация о внутренних параметрах отсутствует или же внутреннее устройство ТО слишком сложно, то ММ такого ТО строят по принципу черного ящика: устанавливают соотношение между внешними и выходными параметрами путем исследования реакции ТО на внешние воздействия.

Теоретический путь построения ММ состоит в установлении связи между у, x и g в виде операторного уравнения:

,   (2.2)

где L – некоторый оператор (в общем случае нелинейный); u – вектор фазовых переменных, включающий те параметры ТО, которые характеризуют его состояние; z – вектор независимых переменных, в общем случае включающий время и пространственные координаты;  0 – нулевой элемент пространства, в котором действует этот оператор,.

Но даже если возможно получить решение уравнения (2.2) и найти зависимость u(z), то далеко не всегда удается представить математическую модель ТО в явном относительно вектора у виде соотношения (2.1). Поэтому именно уравнение (2.2) определяет в общем случае структуру математическую модель ТО, а соотношение (2.1) является более простым частным случаем такой модели.