Расчет угловых швов всех типов (см. рис. 2.3) унифицирован и производится по единым формулам. При действии силы ![]() условия прочности имеют вид
условия прочности имеют вид
![]() ; (2.3)
; (2.3)
![]() . (2.4)
. (2.4)
Формулы (2.3) и (2.4) относятся непосредственно к фланговым швам, а к лобовым швам применяются условно.
Примечание: В лобовых швах возникают как нормальные напряжения (![]() ), так и касательные (τ). Сопротивление стали срезу меньше, чем деформации растяжения (сжатия). Кроме того, в опасном сечении нормальных лобовых швов сдвигающая сила равна
), так и касательные (τ). Сопротивление стали срезу меньше, чем деформации растяжения (сжатия). Кроме того, в опасном сечении нормальных лобовых швов сдвигающая сила равна ![]() , а так же действует точно такая же растягивающая сила. Следовательно, полное напряжение, т.е. равнодействующая
, а так же действует точно такая же растягивающая сила. Следовательно, полное напряжение, т.е. равнодействующая ![]() и
и ![]() , равно
, равно ![]() . Поэтому лобовые швы условно рассчитывают по касательным напряжениям на срез.
. Поэтому лобовые швы условно рассчитывают по касательным напряжениям на срез.
Расчет на прочность фланговых швов
Основными напряжениями фланговых швов при нагружении силой F являются касательные напряжения (τ) в сечении ![]() (рис/ 2.8). По длине шва напряжения τ распределены неравномерно. На концах они больше, чем в середине шва. С увеличением длины фланговых швов и разности податливостей соединяемых элементов возрастает неравномерность распределения напряжений, поэтому длина этих швов ограничена. Расчет таких швов выполняют по среднему напряжению τ:
(рис/ 2.8). По длине шва напряжения τ распределены неравномерно. На концах они больше, чем в середине шва. С увеличением длины фланговых швов и разности податливостей соединяемых элементов возрастает неравномерность распределения напряжений, поэтому длина этих швов ограничена. Расчет таких швов выполняют по среднему напряжению τ:
![]() . (2.5)
. (2.5)
В тех случаях, когда короткие фланговые швы не достаточны для выполнения условия равнопрочности, соединение усиливают прорезными швами (рис. 2.9) или лобовым швом. Условие прочности (2.5) соединения с прорезным швом при ![]() примет вид:
примет вид:
![]() ,
,
где ![]() – длина прорезного шва.
– длина прорезного шва.
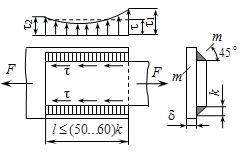
Рис. 2.8. Соединение фланговыми швами
Фланговые швы следует располагать так, чтобы они были нагружены равномерно и не вызывали изгиба соединяемых элементов. Поэтому сварку симметричных элементов следует проводить симметрично расположенными швами.
При сварке несимметричных профилей (рис. 2.10) предполагается, что сила F проходит через центр тяжести поперечного сечения несимметричного профиля. В данном случае нагрузка на фланговые швы распределяется по правилу рычага:
![]() ;
; ![]() ,
,
где ![]() и
и ![]() – нагрузки, действующие на швы;
– нагрузки, действующие на швы; ![]() и
и ![]() – расстояние от центра тяжести поперечного сечения несимметричного профиля до центров тяжести сечений швов.
– расстояние от центра тяжести поперечного сечения несимметричного профиля до центров тяжести сечений швов.
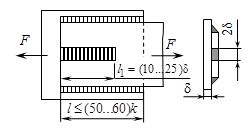
Рис. 2.9. Соединение фланговыми и прорезным швами
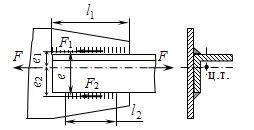
Рис. 2.10. Соединение несимметричных профилей
Швы рассчитывают по соответствующим нагрузкам, следовательно, длины швов будут пропорциональны этим нагрузкам. Для равнобоких уголков приближенно принимают:
![]() (2.6)
(2.6)
где ![]() – общая длина фланговых швов.
– общая длина фланговых швов.
Если соединение нагружено моментом (М), действующим в плоскости стыка соединяемых элементов (рис. 2.11), то напряжение от момента распределяется по длине флангового шва неравномерно, а их векторы направлены различно (рис. 2.11, а). Напряжения ![]() пропорциональны плечам
пропорциональны плечам ![]() и перпендикулярны к ним. Неравномерность распределения напряжений тем больше, чем больше отношение
и перпендикулярны к ним. Неравномерность распределения напряжений тем больше, чем больше отношение ![]() . В общем случае максимальное напряжение можно определить по формуле:
. В общем случае максимальное напряжение можно определить по формуле:
![]() ,
,
где ![]() – полярный момент сопротивления сечения швов в плоскости разрушения, мм3.
– полярный момент сопротивления сечения швов в плоскости разрушения, мм3.
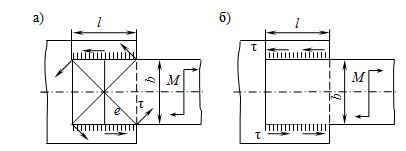
Рис. 2.11. Нагружение фланговых швов моментом
![]() Для сравнительно коротких швов (
Для сравнительно коротких швов (![]() ), распространенных на практике, условно полагают, что напряжения направлены вдоль фланговых швов и распределены по длине швов равномерно (рис. 2.11, б). В данном случае проводится приближенный расчет на прочность по формуле:
), распространенных на практике, условно полагают, что напряжения направлены вдоль фланговых швов и распределены по длине швов равномерно (рис. 2.11, б). В данном случае проводится приближенный расчет на прочность по формуле:
![]() . (2.7)
. (2.7)
Расчет на прочность лобовых швов
Напряженное состояние лобового шва неоднородно. Происходит значительная концентрация напряжений, связанная с резким изменением сечений соединяемых элементов в месте сварки и эксцентричным приложением нагрузки. Основными являются касательные напряжения (τ) в плоскости стыка элементов и нормальные напряжения (σ) в перпендикулярной плоскости.
В инженерной практике принято рассчитывать на прочность лобовые швы только по касательным напряжениям (τ). За расчетное сечение так же, как и во фланговых швах, принимают сечение по биссектрисе прямого угла (см. рис. 2.5). Как подтверждает практика, именно по этому сечению происходит разрушение шва. В данном случае при действии силы F (см. рис. 2.3, а; здесь длина шва l равна ширине соединяемых элементов b) условие прочности имеет вид (2.3) или (2.4).
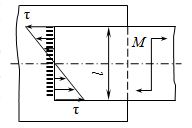
Рис. 2.12. Нагружение лобового шва моментом М
При нагружении лобового шва моментом M, действующим в плоскости стыка соединяемых элементов (рис. 2.12), расчет на прочность носит также условный характер. Условие прочности на срез в данном случае записывают по аналогии с условием прочности на изгиб:
![]() .
.
При совместном действии силы (F) и момента (M) условие прочности лобового шва имеет вид:
![]() .
.
Расчет на прочность комбинированных швов
Расчет на прочность комбинированных соединений лобовыми и фланговыми швами носит приближенный характер и основан на следующих допущениях:
· швы работают независимо;
· фланговые швы короткие и передают только силы, направленные вдоль своей оси;
· катет шва (k) мал по сравнению с размером b.
При нагружении комбинированных швов силой F (рис. 2.13, а) условие прочности имеет вид:
![]() (2.8)
(2.8)
При нагружении комбинированных швов моментом (M) (рис. 2.13, б) в соответствии с принятыми допущениями внешний момент (M) уравновешивается парой сил во фланговых швах ![]() и моментом лобового шва
и моментом лобового шва ![]() :
:
![]() .
.
Отсюда
![]() (2.9)
(2.9)
При ![]() формула (2.9) принимает вид:
формула (2.9) принимает вид:
![]() . (2.10)
. (2.10)
Ввиду своей простоты формула (2.10) может быть использована и при проектном расчете.
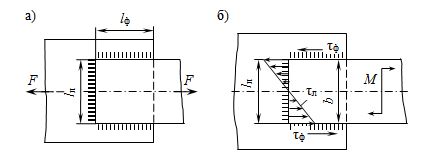
Рис. 2.13. Комбинированные соединения лобовым и фланговыми швами
При совместном действии на комбинированный шов силы (F) и момента (M) условие прочности имеет вид:
![]() ,
,
где ![]() – касательное напряжение от действия силы F, определяемое по формуле (2.8);
– касательное напряжение от действия силы F, определяемое по формуле (2.8); ![]() – касательное напряжение от действия момента (M), определяемое по формулам (2.9) или (2.10).
– касательное напряжение от действия момента (M), определяемое по формулам (2.9) или (2.10).