Графический метод используется для решения задач линейного программирования с двумя переменными, заданными в симметричной форме, и многими переменными, заданными в канонической форме (при условии, что они содержат не более двух свободных переменных).
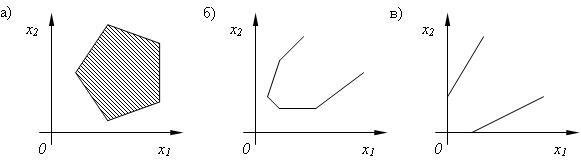
Рис. 2.1. Области допустимых решений задачи:
а- выпуклый многоугольник, б – выпуклая многоугольная область, в – пустое множество
Задачу линейного программирования с двумя переменными можно записать так:
![]() (2.5)
(2.5)
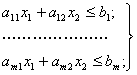 (2.6)
(2.6)
![]() (2.7)
(2.7)
Область допустимых решений задачи (2.5) – (2.7) представляет собой либо выпуклый многоугольник (рис. 2.1, а), либо выпуклую многоугольную область (рис. 2.1, б), либо пустое множество (рис. 2.1, в). Возможно также, что допустимая область состоит из единственной точки.
Функция (2.5) представляет собой на плоскости ![]() семейство параллельных прямых, каждой из которых отвечает определенное значение
семейство параллельных прямых, каждой из которых отвечает определенное значение ![]() . Перпендикулярный к этим прямым вектор
. Перпендикулярный к этим прямым вектор ![]() указывает направление наискорейшего возрастания функции
указывает направление наискорейшего возрастания функции ![]() (рис. 2.2), и задача (2.5) – (2.7) заключается в следующем: необходимо
(рис. 2.2), и задача (2.5) – (2.7) заключается в следующем: необходимо
найти точку допустимой области, через которую проходит прямая семейства ![]() , отвечающая наибольшему значению функции (рис. 2.3, а).
, отвечающая наибольшему значению функции (рис. 2.3, а).
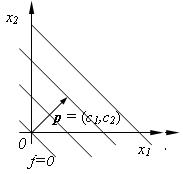
Рис. 2.2. Направление вектора p
При решении задачи линейного программирования графическим способом могут встретиться следующие случаи: задача имеет единственное решение (см. рис. 2.3, а); задача имеет бесконечное множество решений (рис. 2.3, б); функция ![]() не имеет экстремального значения (рис. 2.3, в).
не имеет экстремального значения (рис. 2.3, в).
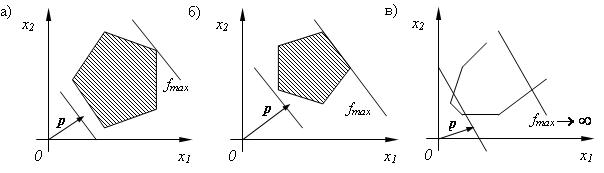
Рис. 2.3. Варианты решения задачи:
А – единственное решение, б – бесконечное множество решений, в – не существует экстремального значения
Пример 3
Для сохранения здоровья и работоспособности человек должен потреблять в сутки определенное количество питательных веществ: белков, жиров, витаминов. Запасы их в продуктах П1 и П2 неодинаковы. Количество соответствующего вещества в единице каждого продукта представлено в табл. 2.1.
Таблица 2.1 Количество необходимых питательных веществ в продуктах
|
Питательные вещества |
Минимальная норма |
Содержание питательного вещества в 1 ед. продукта, усл. ед. |
|
|
П1 |
П2 |
||
|
Белки Жиры Витамины |
120 70 10 |
0,2 0,075 0 |
0,1 0,1 0,1 |
Стоимость 1 ед. продукта: П1 – 0,2 руб.; П2 – 0,3 руб.
Требуется так организовать питание, чтобы стоимость его были наименьшей, а организм получил не менее минимальной суточной нормы потребления питательных веществ всех видов.
Решение
Обозначим через ![]() количество продукта П1, а через
количество продукта П1, а через ![]() – количество продукта П2, которые предполагается включить в рацион.
– количество продукта П2, которые предполагается включить в рацион.
Количество белков, содержащихся в рационе ![]() , можно выразить суммой:
, можно выразить суммой:
![]() .
.
По условию задачи эта величина не может быть меньше 120 ед., т.е.
![]() . (2.8)
. (2.8)
Ограничения по содержанию в рационе жиров и витаминов примут вид:
![]() (2.9)
(2.9)
![]() . (2.10)
. (2.10)
Естественно, что величины ![]() и
и ![]() (количество продукта каждого вида) выражаются неотрицательными числами, т.е.
(количество продукта каждого вида) выражаются неотрицательными числами, т.е.
![]() . (2.11)
. (2.11)
Стоимость рациона можно выразить в виде следующей функции:
![]() . (2.12)
. (2.12)
Задача сводится к определению таких значений ![]() и
и ![]() , удовлетворяющих линейным ограничениям (2.8) — (2.11), при которых линейная функция (2.12) достигает наименьшего значения.
, удовлетворяющих линейным ограничениям (2.8) — (2.11), при которых линейная функция (2.12) достигает наименьшего значения.
Для построения области допустимых решений задачи строим соответствующие данным неравенствам граничные прямые (рис. 2.4):
![]() ;
;
![]() ;
;
![]()
или
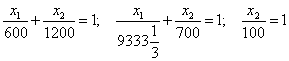 .
.
При второй записи уравнений сразу определяются величины отрезков, которые отсекаются прямыми на осях координат (рис. 2.4).
Затем находим полуплоскости, в которых выполняются неравенства (2.8) — (2.11):
· неравенство (2.8) определяет полуплоскость с граничной прямой 1, к которой точка ![]() не принадлежит, так как
не принадлежит, так как
![]() ;
;
· неравенство (2.9) – полуплоскость с граничной прямой 2, к которой точка ![]() не принадлежит, так как
не принадлежит, так как
![]() ;
;
· неравенство (2.10) – полуплоскость с граничной прямой 3, к которой точка ![]() не принадлежит, так как
не принадлежит, так как
![]() .
.
С учетом неравенства (2.11) область допустимых решений представляет собой неограниченную многоугольную область с вершинами А, В, С.
Далее строим направляющий вектор ![]() и перпендикулярно к нему прямую семейства
и перпендикулярно к нему прямую семейства ![]() , например
, например ![]() (см. рис. 2.4). Параллельным перемещением вспомогательной прямой
(см. рис. 2.4). Параллельным перемещением вспомогательной прямой ![]() находим точку С (первая встретившаяся вершина), в которой функция
находим точку С (первая встретившаяся вершина), в которой функция ![]() достигает наименьшего значения.
достигает наименьшего значения.
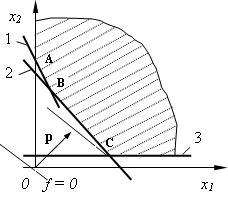
Рис.2.4. Графическое решение задачи
Для того чтобы найти координаты точки С, решим совместно уравнения граничных прямых 1, 3, на пересечении которых лежит точка С. Получим:
![]() ,
,
при этом
![]() ,
,
т.е. в состав оптимального суточного рациона следует включить 800 ед. продукта П1 и 100 ед. продукта П2. Стоимость такого рациона будет наименьшей и составит 190 руб.