Определение. Вершина w орграфа D (графа G) достижима из вершины v, если либо v=w, либо существует путь из v в w (маршрут, соединяющий v, w).

Дадим более удобное определение связных графов.

Определение. Граф называется связным, если для любых двух его вершин v, w существует простая цепь из v в w.

Определение. Граф (орграф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v, w (из v и w).

Определение. Орграф называется односторонне связным, если для любых его двух вершин, по крайней мере, одна достижима из другой.

Определение. Если граф не является связным, то он называется несвязным.

Определение. Компонентой связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа.

В дальнейшем количество компонент связности графа будем обозначать k.

Пример 79.

Данный граф не является связным: k = 3.

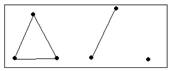
Данный граф является связным: k = 0.

Теорема. Пусть G – простой граф с n вершинами и k компонентами. Тогда число m его ребер удовлетворяет неравенствам

Следствие. Любой простой граф с n вершинами и более чем (т-1)(т-2)/2 ребрами связен.

При исследовании графов возникает вопрос: насколько сильно связен связный граф? Этот вопрос можно сформулировать и так: сколько ребер нужно удалить из графа, чтобы он перестал быть связным? Под операцией удаления вершин из графа будем понимать операцию, заключающуюся в удалении некоторой вершины вместе с инцидентными ей ребрами.

Определение. Вершина графа, удаление которой увеличивает число компонент связности, называется разделяющейся.

Определение. Разделяющим множеством связного графа G называется такое множество его ребер, удаление которого приводит к несвязному графу.

Определение. Разрезом называется такое разделяющее множество, никакое собственное подмножество которого не является разделяющим.

Определение. Разрез, состоящий из одного ребра, называется мостом (перешейком).

Пример 80.

Для графа, изображенного на рис. 3.15, каждое из множеств {e₁, e₂, e₅} и {e₃, e₆, e₇, e₈} является разделяющим.

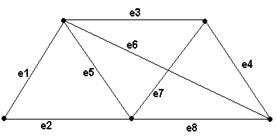
Рис. 3.15. Граф для примера 80

Разрезом является множество ребер {e₁, e₂}.

В графе возможно выделить несколько разделяющих множеств и разрезов.