Определение. Назовём орграф  нагруженным, если на множестве дуг  определена некоторая функция  , которую часто называют весовой функцией.

Тем самым в нагруженном орграфе  каждой дуге поставлено в соответствие некоторое дей­ствительное число . Значение  будем называть длиной дуги .

Для любого пути нагруженного орграфа обозначим через сумму длин входящих в дуг, при этом каждая дуга учитывается столько раз, сколько она входит в путь. Величину будем называть длиной пути  в нагруженном орграфе. Ранее так называлось количество дуг в пути . В связи с этим заметим, что если длины дуг выбраны равными 1, товы­ражает введенную ранее длину пути  в ненагруженном орграфе. Следовательно, любой ненагруженный орграф можно считать на­груженным с длинами дуг, равными 1. Аналогично определяется и нагруженный граф, а также длина маршрута в нем.

Определение. Путь в нагруженном орграфе  из вершины  в вершину , где , называется минимальным, если он имеет минималь­ную длину среди всех путей орграфа  из  в . Аналогично определяется и минимальный маршрут в нагруженном графе .

Рассмотрим теперь задачу поиска минимальных путей (мар­шрутов) в нагруженном орграфе (графе). При этом для опреде­ленности рассуждения будем проводить для орграфа (для гра­фа они аналогичны).

Пусть  — нагруженный орграф, , . Введем величины , где , …, , , ,… Для каждых фиксированных  и  величина  равна длине минималь­ного пути среди путей из  в , содержащих не более  дуг; если же таких путей нет, то =. Кроме того, если произ­вольную вершину считать путем из ₁ в _i нулевой длины, то величины  можно ввести также и для , при этом

 (1)

Введем также в рассмотрение квадратную матрицу  порядка  с элементами

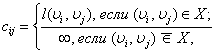
которую будем называть матрицей длин дуг нагруженного орграфа.

Следующее утверждение дает простые формулы для вычисле­ния величин .

Утверждение.  

  .

Используя данное утверждение, нетрудно описать алгоритм нахождения таблицы значений величин  (будем записывать её в виде матрицы, где - номер строки,  — номер столбца). Действительно, используя рекуррентные соотношения (2), (3) и исходя  из (1), последовательно определяем набор величин  (()-й столбец матрицы), начиная с , а затем шаг за шагом увеличиваем значение  до любой необходимой величины.

Алгоритм Форда – Беллмана нахождения минимального пути

в нагруженном орграфе  из  в  

Шаг 1. Пусть мы уже составили таблицу величин . Если  не достижима из  (предполагаем, что все величины  конечны). В этом случае работа алгоритма заканчивается.

Шаг 2. Пусть . Тогда число  выражает длинны любого минимального пути из  в в нагруженном орграфе . Определим минимальное число , при котором выполняется равенство . По определению чисел  получим, что  — минимальное число дуг в пути среди всех минимальных путей из  в  в нагруженном орграфе .

Шаг 3.  Последовательно определяем номера  такие что

. . . . . .                                   (4)

Из (4) с учётом того, что , имеем , откуда, используя (1), получаем

 (5)

Складывая равенства (4) и учитывая (5), имеем

т.е. - искомый минимальный путь из  в в нагруженном орграфе . Заметим, что в этом пути ровно  дуг Следовательно, мы определили путь с минимальным числом дуг среди всех минимальных путей из  в  в нагруженном оргра­фе .

Замечание. Номера , удовлетворяющие (4) вообще говоря, могут быть выделены неоднозначно. Эта неодно­значность соответствует случаям, когда существует несколько различных путей из   в  с минимальным числом дуг среди минимальных путей из  в  в нагруженном орграфе .

Замечание. Алгоритм  можно модифицировать, с тем чтобы определить минимальный путь из  в заданную вершину  среди путей из  в , содержащих не более  дуг, где - заданное число, . Для этого в алгоритме  вместо  следует воспользоваться .

Пример 83.

Определить минимальный путь из v₁ в v₆ в нагруженном орграфе D, изображенном на рис. 3.17.

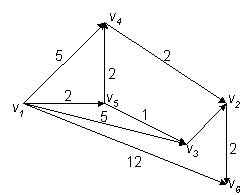
Рис. 3.17. Нагруженный орграф для примера 83

Решение.

Составим матрицу C(D) длин дуг нагруженного орграфа D (табл. 3.3). Справа от матрицы C(D) припишем шесть столбцов, которые будем определять, используя  рекуррентное соотношение (2) и исходя из (1).

Величина  выражает длину минимального пути из v₁ в v₆ в нагруженном орграфе D. Найдем минимальное число , при котором выполняется равенство . Получаем, что k₁ = 4. Таким образом, минимальное число дуг в пути среди всех минимальных путей из v₁ в v₆ в нагруженном графе D равняется 4. Определим теперь последовательность номеров i₁, i₂, i₃, i₄, i₅, где i₁ = 6, удовлетворяющих (4) (для этого используем формулу (2)).

Таблица 3.3 Матрица длин дуг нагруженного орграфа

Получаем, что в качестве такой последовательности надо взять номера 6, 2, 3, 5, 1, так как

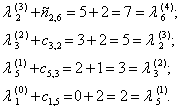
Тогда v₁v₅v₃v₂v₆ – искомый минимальный путь из v₁ в v₆ в нагруженном орграфе D, причем он содержит минимальное число дуг среди всех возможных минимальных путей из v₁ в v₆ .