Применение операционного исчисления к решению конкретных задач укладывается в общую схему. Пусть требуется найти результат ![]() , для получения которого (без применения операционного метода) надо над заданной функцией f(t) выполнить какую-то операцию А.
, для получения которого (без применения операционного метода) надо над заданной функцией f(t) выполнить какую-то операцию А.
Применяя операционный метод, сначала переходят от оригинала f(t) к его изображению F(p); затем над изображением выполняют операцию В, соответствующую в операционном методе операции А. Например, умножают изображение на p вместо дифференцирования f(t), получают промежуточный результат – новое изображение Ф(р); наконец, переходят от изображения Ф(р) к искомому оригиналу ![]() .
.
Итак, общая схема решения задачи удлиняется. Однако при этом получается значительный выигрыш как в средствах вычислений, так и во времени. Этот выигрыш достигается путем широкого использования основных теорем метода, его свойств, таблиц соответствий, введенияначальных условий в состав изображений производных, результатов ТФКП.
Линейные дифференциальные уравнения составляют наиболее разработанную часть теории дифференциальных уравнений. Дифференциальные уравнения описывают реальные процессы, что делает их ценными для многочисленных приложений[12]. Здесь рассмотрим решения линейных дифференциальных уравнений с постоянными коэффициентами. Суть в том, что эти уравнения имеют первостепенное значение при изучении механических и электрических систем, основные параметры которых (сопротивление, индуктивность, моменты инерции и т.д.) не зависят от времени, а также токов, напряжений, перемещений и т.п.
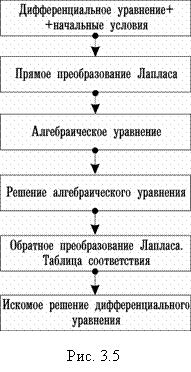
Операторный метод задачу интегрирования дифференциального уравнения сводит к алгебраической задаче, что намного упрощает дело. Приведем алгоритм решения (рис. 3.5) дифференциальных уравнений операционным методом [13]. Покажем действие алгоритма на примерах.
Пример 1
Найти частное решение уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() .
.
Решение. Найдем изображающее уравнение У(р) (изображение искомого решения ![]() ). Пусть
). Пусть ![]()
![]() У(р), тогда
У(р), тогда
![]()
![]()
![]()
На основании теоремы единственности получим алгебраическое уравнение относительно У(р), в котором учтено начальное условие:
![]()
Решаем это алгебраическое уравнение относительно У(р):
![]() .
.
Определяем оригинал y(t) – частное решение (решение задачи Коши [14]) по таблице соответствий (табл. 3.1):
![]() .
.
Рекомендуется делать неполную проверку, а именно: при t = 0 должно быть y(0) = 1, что имеет место.
Пример 2
Решить уравнение ![]() , y(0) = 1,
, y(0) = 1, ![]() .
.
Решение. По алгоритму (рис. 3.5) получим:
![]()
или ![]() .
.
Отсюда
![]() .
.
Пользуясь теоремой свертывания, найдем оригинал для второго слагаемого:
![]()
![]() 1;
1; ![]() ;
;![]()
![]()
и 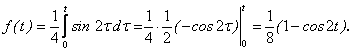
Переходя от изображений к оригиналам, окончательно получим:
![]()
Пример 3
Найти частное решение уравнения ![]() , удовлетворяющего начальным условиям y(0) = 1, y’(0) = -1.
, удовлетворяющего начальным условиям y(0) = 1, y’(0) = -1.
Решение. Согласно (рис. 3.5) получим:
![]() ,
,
откуда
![]() .
.
Корни знаменателя: ![]()
![]()
Применяя вторую теорему разложения (3.36), получим:
![]() .
.
Как отмечалось ранее, можно правильную рациональную дробь разложить на сумму простейших дробей:

Приравнивая коэффициенты при одинаковых степенях р, получим систему уравнений:
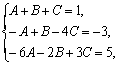
решая которую, находим: ![]() (проверьте). Следовательно,
(проверьте). Следовательно,
![]() .
.
Используя свойство линейности (3.5) и таблицу соответствий (табл. 3.1) получим:
![]()
Методическое указание
Так же выполняется решение систем обыкновенных линейных уравнений. Системы преобразуются к системам алгебраических линейных уравнений, относительно изображений искомых функций. Оригиналы этих решений находят как обычно, используя свойства метода или таблицы соответствий. Покажем это на примере.
Пример 4
Решить систему уравнений:
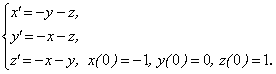
Решение. Пусть: x(t)![]() X(p), y(t)
X(p), y(t) ![]() У(p), z(t)
У(p), z(t) ![]() Z(p). Применив к каждому уравнению преобразование Лапласа (3.1) и, учтя начальные условия, получим систему алгебраических линейных уравнений относительно изображений искомых функций:
Z(p). Применив к каждому уравнению преобразование Лапласа (3.1) и, учтя начальные условия, получим систему алгебраических линейных уравнений относительно изображений искомых функций:

Решим её по правилу Крамера:
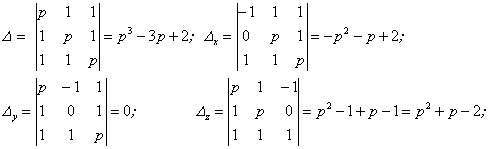
![]()
Или
![]()
![]()
По таблице соответствий (табл. 3.1) окончательно получим:
![]()
Рекомендуется выполнить проверку самостоятельно.
Задачи для упражнений
1) Найти частные решения дифференциальных уравнений, удовлетворяющих заданным начальным условиям:
а) ![]() Ответ:
Ответ: ![]() .
.
б) ![]() Ответ:
Ответ: ![]() .
.
в) ![]() Ответ:
Ответ: ![]() .
.
г) ![]() Ответ:
Ответ: ![]()
д) ![]() Ответ:
Ответ: ![]() .
.
2) Решить систему дифференциальных уравнений:
а) 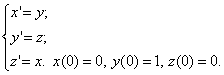
Ответ:
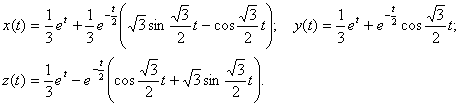
б) 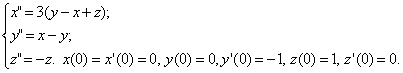
Ответ:
![]()
![]()
в) 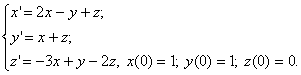
Ответ:
![]()
г) ![]()
Ответ:
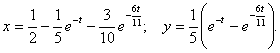
д) ![]()
Ответ:
![]()