В любом заданном множестве данных неизбежно будет рассеяние. Даже те несколько факторов, относительно которых мы предполагаем, что они постоянны, на самом деле не будут совершенно неизменными. Хотя сами значения все время меняются, они подчиняются некоторому правилу, а в таком случае говорят, что данные следуют определенному распределению. В контроле качества мы стремимся на основе собранных данных выявить факты, а затем, опираясь на эти факты, предпринять необходимые действия. Сбор данных — не самоцель, но средство отыскания тех фактов, которые стоят за данными. Пример — управление промышленным процессом с помощью контрольной карты средних — размахов, ![]() , Наша цель заключается не в определении характеристики выборки, взятой для нанесения на карту, а в том, чтобы выяснить, в каком состоянии находится сам процесс.
, Наша цель заключается не в определении характеристики выборки, взятой для нанесения на карту, а в том, чтобы выяснить, в каком состоянии находится сам процесс.
Вся совокупность рассматриваемых объектов называется генеральной совокупностью (популяцией). Один или несколько элементов, взятых из генеральной совокупности для получения информации о ней, называется выборкой. Так как выборка используется для оценивания характеристик всей генеральной совокупности, ее стоит выбирать таким образом, чтобы она отражала именно эти характеристики. Распространенный выборочный метод заключается в выборе любого члена генеральной совокупности с одинаковой вероятностью. Этот метод называют случайным выбором, а выборку, полученную случайным выбором, — случайной выборкой. При этом получаем данные, измеряя характеристики выборки. Пользуясь этими данными, мы делаем выводы относительно генеральной совокупности, а затем производим корректирующие действия. Правда, измеренные выборочные значения будут варьировать от выборки к выборке, затрудняя решение о необходимом действии. Статистический анализ должен подсказать нам, как интерпретировать такие данные.
Данные, полученные из выборки, служат основой для решений о генеральной совокупности. Чем больше объем выборки, тем больше информации об этой совокупности мы получим. Но рост объема выборки одновременно означает и рост количества данных, что затрудняет понимание совокупности по этим данным, даже если они табулированы. В таком случае нам нужен метод, благодаря которому мы могли бы понимать генеральную совокупность с первого взгляда. Нашим требованиям отвечает гистограмма.
Построим гистограмму для исследования распределения диаметров стальных осей, полученных на токарном станке. Измерено 90 осей, результаты представлены в табл. 3.4.
Этапы построения диаграммы.
Этап 1. Вычисление выборочного размаха (R). Получите наибольшее и наименьшее выборочные значения и вычислите R = (наибольшее наблюдаемое значение) — (наименьшее наблюдаемое значение).
В табл. 3.4 сначала надо вычислить наибольшее и наименьшее значения в каждой строке таблицы исходных данных, а затем взять самое большое из максимумов и самое маленькое из минимумов.
Таблица 3.4
Исходные данные диаметров осей
|
Номер выборки |
Результаты измерений |
|||||||||
|
1-10 |
2,510 |
2,517 |
2,522 |
2,510 |
2,511 |
2,519 |
2,532 |
2,543 |
2,525 |
2,522 |
|
11-20 |
2,527 |
2,536 |
2,506 |
2,541 |
2,512 |
2,515 |
2,521 |
2,536 |
2,529 |
2,524 |
|
21-30 |
2,529 |
2,523 |
2,523 |
2,523 |
2,519 |
2,528 |
2,543 |
2,538 |
2,518 |
2,534 |
|
31-40 |
2,520 |
2,514 |
2,512 |
2,534 |
2,526 |
2,530 |
2,532 |
2,526 |
2,523 |
2,520 |
|
41-50 |
2,535 |
2,523 |
2,526 |
2,525 |
2,532 |
2,522 |
2,502 |
2,530 |
2,522 |
2,514 |
|
51-60 |
2,533 |
2,510 |
2,542 |
2,524 |
2,530 |
2,521 |
2,522 |
2,535 |
2,540 |
2,528 |
|
61-70 |
2,525 |
2,515 |
2,520 |
2,519 |
2,526 |
2,527 |
2,522 |
2,542 |
2,540 |
2,528 |
|
71-80 |
2,531 |
2,545 |
2,524 |
2,522 |
2,520 |
2,519 |
2,519 |
2,529 |
2,522 |
2,513 |
|
81-90 |
2,518 |
2,527 |
2,511 |
2,519 |
2,531 |
2,527 |
2,529 |
2,528 |
2,519 |
2,521 |
Этап 2. Определение размеров классов. Размеры классов определяются так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Для получения ширины интервалов R делят на 1,2 или 5 (либо 10, 20, 50; 0,1, 0,2, 0,5 и т.д.), чтобы получилось от 5 до 20 интервалов равной ширины.
Этап 3. Подготовка бланка таблицы частот. Готовится бланк (табл. 3.5), куда можно занести класс, среднюю точку, отметки частот, частоты и т.д.
Этап 4. Определение границ класса. Определите границы интервалов так, чтобы они включали наименьшее и наибольшее значения и положите их в основу таблицы частот. Сначала определите нижнюю границу первого класса и прибавьте к ней ширину этого класса, чтобы получить границу между первым и вторым классами. Как только вы это сделаете, можно будет удостовериться, что первый класс включает наименьшее значение и что его граничное значение приходится на середину принятой единицы измерения (т.е. на число 5 в следующем десятичном разряде). Далее, продолжая прибавлять найденный интервал к предыдущему значению для получения второй границы, затем третьей и т.д., можно удостовериться, что последний класс включает максимальное значение.
Этап 5. Вычисление середины класса. Средняя точка класса определяется полусуммой нижней и верхней границ класса.
Этап 6. Получение частот. Прочтите наблюденные значения одно за другим и запишите частоты, приходящиеся на каждый интервал, используя наклонные черточки, сгруппированные по пять.
Этап 7. Возьмите лист бумаги в клеточку, нанесите горизонтальную ось и выберите масштаб на этой оси. Не стоит ориентироваться при этом на интервалы классов, гораздо лучше основываться на единицах измерения данных, беря, например, 10 мм как 10 г. Так делается для удобства сравнений множества гистограмм, описывающих похожие факторы и характеристики, а также для сравнения гистограмм с допусками. На горизонтальной оси с обеих сторон (перед первым интервалом и после последнего) оставьте свободное место, приблизительно равное интервалу.
Этап 8. Разметьте левую вертикальную ось масштабом частот, а на правую (если понадобится) нанесите шкалу относительных частот. Высоту класса с максимальной частотой стоит выбирать так, чтобы она оказалась между 0,5 и 2,0 расстояниями от максимума до минимума на горизонтальной оси.
Таблица 3.5
Таблица частот
|
Порядковый номер |
Класс |
Середина класса |
Подсчет частот |
Частота f |
|
1 2 3 4 5 6 7 8 9 |
2,5005-2,5055 2,5055-2,5105 2,5105-2,5155 2,5155-2,5205 2,5205-2,5255 2,5255-2,5305 2,5305-2,5355 2,5305-2,5405 2,5405-2,5455 |
2,503 2,508 2,513 2,518 2,523 2,528 2,533 2,538 2,543 |
/ //// ///// //// ///// ///// //// ///// ///// ///// ///// //// ///// ///// ///// //// ///// ///// ///// ///// / |
1 4 9 14 22 19 10 5 6 |
|
Итого |
90 |
Этап 9. Нанесение на горизонтальную ось границы классов.
Этап 10. Пользуясь интервалом класса как основанием, постройте прямоугольник, высота которого соответствует частоте этого класса.
Этап 11. Нанесите на график линию, представляющую среднее арифметическое, а также линии, представляющие границы допуска, если они есть.
В завершение укажите происхождение ваших данных (период, в течение которого собирались данные и т.п.), число данных n, среднее арифметическое ![]() истандартное отклонение
истандартное отклонение ![]() (рис. 3.7).
(рис. 3.7).
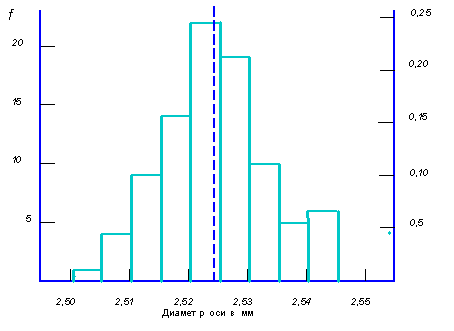
Рис. 3.7. Гистограмма распределения диаметров осей
Полезную информацию о характере популяции можно получить, взглянув на форму гистограммы. Формы, представленные на рис. 3.8–3.13, типичны. Воспользуемся ими как образцами при анализе процессов.
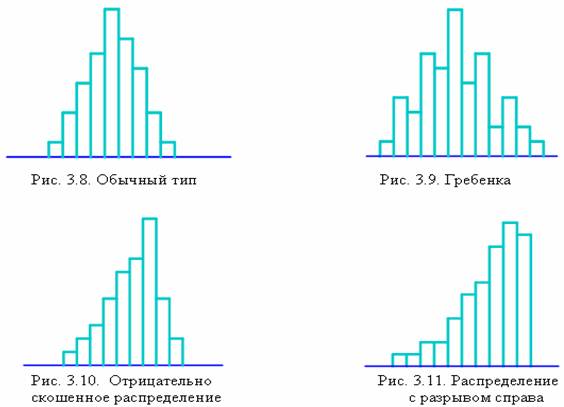
1) Обычный тип (симметричный или колоколообразный) (рис. 3.8). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам. Форма симметрична. Это именно та форма, которая встречается чаще всего.
2) Гребенка (мультимодальный тип) (рис. 3.9). Классы через один имеют более низкие частоты. Такая форма встречается, когда число единичных наблюдений, попадающих в класс, колеблется от класса к классу или когда действует определенное правило округления данных.
3) Положительно скошенное распределение (отрицательно скошенное распределение, рис. 3.10). Среднее значение гистограммы локализуется слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична. Такая форма встречается, когда нижняя (верхняя) граница регулируется либо теоретически, либо по значению допуска или когда левое (правое) значение недостижимо.
4) Распределение с обрывом слева (распределение с обрывом справа) (рис. 3.11). Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты резко спадают при движении влево (вправо) и наоборот, медленно вправо (влево). Форма асимметрична. Это одна из тех форм, которые часто встречаются при 100-процентном просеивании изделий из-за плохой воспроизводимости процесса, а также когда проявляется резко выраженная положительная (отрицательная) асимметрия.
5) Плато (равномерное и прямоугольное распределения) (рис. 3.12). Частоты в
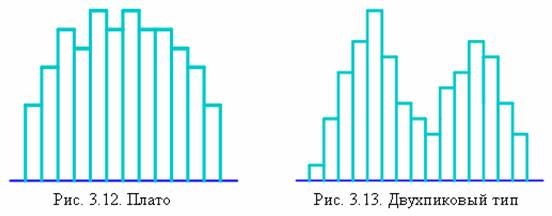
разных классах образуют плато, поскольку все классы имеют более или менее одинаковые ожидаемые частоты с конечными классами. Такая форма встречается в смеси нескольких распределений, имеющих различные средние.
6) Двухпиковый тип (бимодальный тип) (рис. 3.13). В окрестностях центра диапазона данных частота низкая, зато есть по пику с каждой стороны. Такая форма встречается, когда смешиваются два распределения с далеко отстоящими средними значениями.
7) Распределение с изолированным пиком. Наряду с распределением обычного типа, появляется маленький изолированный пик (рис. 3.14). Это форма, которая появляется при наличии малых включений данных из другого распределения, как, скажем, в случае нарушения нормальности процесса, появления ошибки измерения или просто включения данных из другого процесса.
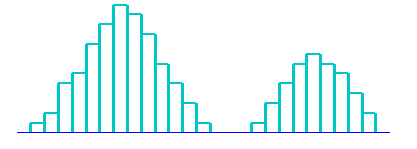
Рис. 3.14. Распределение с изолированным пиком
Если имеются верхнее и нижнее пороговые значения (границы ![]() и
и ![]() ) для показателя по техническим условиям, то можно нанести их на гистограмму, чтобы выполнить сравнение. Тогда вы увидите, хорошо ли располагается гистограмма внутри границ. Эту картину используют при оценивании популяций. Ниже (рис. 3.15 и рис. 3.16) представлены два возможных варианта.
) для показателя по техническим условиям, то можно нанести их на гистограмму, чтобы выполнить сравнение. Тогда вы увидите, хорошо ли располагается гистограмма внутри границ. Эту картину используют при оценивании популяций. Ниже (рис. 3.15 и рис. 3.16) представлены два возможных варианта.
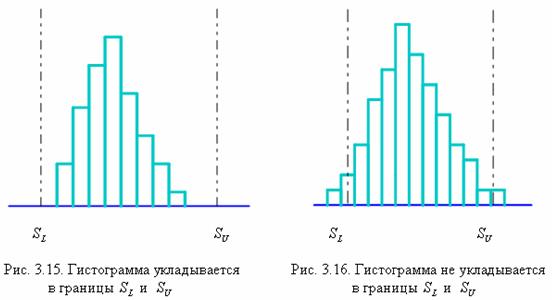
Когда гистограмма укладывается внутри границ![]() и
и![]() , требуется только поддержание существующего состояния (рис. 3.14). Если гистограмма не укладывается внутри границ
, требуется только поддержание существующего состояния (рис. 3.14). Если гистограмма не укладывается внутри границ ![]() и
и ![]() , потребуются меры, направленные на снижение вариации и смещение среднего ближе к центру поля допуска.
, потребуются меры, направленные на снижение вариации и смещение среднего ближе к центру поля допуска.
Представленные в гистограммах характеристики качества промышленной продукции имеют случайную природу. Как для всякой случайной величины, мерой для представления центра данных служит среднее арифметическое, или математическое ожидание (ожидаемое значение). Когда у нас есть п отдельных значений ![]() ,…
,…![]() среднее таких данных дается выражением
среднее таких данных дается выражением
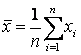 ,
,
но для множества как целого среднее определяется выражением
![]() ,
,
где P(x)-вероятность случайной величины x.
Величина ![]() - среднее арифметическое полученных данных, она называется выборочным средним. Величина
- среднее арифметическое полученных данных, она называется выборочным средним. Величина ![]() — среднее арифметическое всего множества, которое мы рассматриваем, она называется генеральным средним.
— среднее арифметическое всего множества, которое мы рассматриваем, она называется генеральным средним.
Дисперсия и стандартное отклонение принадлежат к мерам, используемым для выражения степени концентрации данных относительно их центра. Когда у нас есть п отдельных значений ![]() ,…
,…![]() , их дисперсия дается выражением
, их дисперсия дается выражением
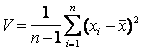 ,
,
стандартное отклонение –
![]() .
.
Дисперсия генеральной совокупности получается из формулы
![]() ,
,
а стандартное отклонение, которое представляет собой корень квадратный из дисперсии, обозначается через ![]() . Большая дисперсия означает большое рассеяние в данных. Величины V и
. Большая дисперсия означает большое рассеяние в данных. Величины V и ![]() — значения, получаемые из имеющихся данных, они называются выборочной дисперсией и выборочным стандартным отклонением, соответственно. Величины
— значения, получаемые из имеющихся данных, они называются выборочной дисперсией и выборочным стандартным отклонением, соответственно. Величины ![]() и
и ![]() - значения, относящиеся к генеральной совокупности, их называют генеральной дисперсией и генеральным стандартным отклонением, соответственно. Вычисление указанных величин выполняют с помощью различных вычислительных средств.
- значения, относящиеся к генеральной совокупности, их называют генеральной дисперсией и генеральным стандартным отклонением, соответственно. Вычисление указанных величин выполняют с помощью различных вычислительных средств.
Всякая гистограмма строится на основе некоторого числа данных. Но что произойдет с гистограммой, если мы станем наращивать число данных? Если интервал класса по мере роста числа данных будет все меньше и меньше, то сглаженная кривая распределения частот получится как предел распределения относительных частот. Она как раз и станет представлением для самой генеральной совокупности, поскольку получается из бесконечного числа данных.
Есть множество видов распределений, но самое типичное из них — нормальное распределение. Когда разброс характеристики качества обусловлен суммой большого числа независимых неограниченных ошибок, вызванных различными факторами, то распределение этой характеристики качества во многих случаях получается приблизительно нормальным. Нормальное распределение можно легко узнать по колоколообразной или вершиноподобной форме либо при более подробном описании: а) его наибольшая частота приходится на середину интервала и плавно спадает к его концам
(хвостам), б) оно симметрично. Математически эту кривую можно представить следующим образом:
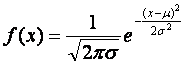 .
.
Нормальное распределение имеет два параметра ![]() и
и ![]() . Эти параметры однозначно определяют нормальное распределение, которое поэтому обозначается просто как N(
. Эти параметры однозначно определяют нормальное распределение, которое поэтому обозначается просто как N(![]() ). Сами параметры имеют следующий смысл:
). Сами параметры имеют следующий смысл: ![]() — центр распределения (среднее арифметическое);
— центр распределения (среднее арифметическое); ![]() - разброс распределения (стандартное отклонение). Их можно представить графически (рис. 3.17).
- разброс распределения (стандартное отклонение). Их можно представить графически (рис. 3.17).
Для подсчета вероятностей в нормальном распределении мы его стандартизуем и пользуемся таблицами нормального распределения. Стандартизация — это преобразование случайной величины х к u:
![]() .
.
Тогда мы получаем стандартную меру u , распределенную как стандартное (нормированное) нормальное распределение ![]() . Указанное распределение представлено в справочниках.
. Указанное распределение представлено в справочниках.
Определим вероятность того, что случайная величина х из распределения N(![]() ) окажется в пределах
) окажется в пределах ![]() . На рис. 3.17 показаны вероятности для различных значений и. Теоретически нормальная переменная может принимать любое значение от -
. На рис. 3.17 показаны вероятности для различных значений и. Теоретически нормальная переменная может принимать любое значение от -![]() до +
до +![]() . Но из рисунка видно, что уже для и = 3 вероятность составит 99,7 %. Это означает, что на практике мы можем пренебречь шансами, что х окажется за пределами
. Но из рисунка видно, что уже для и = 3 вероятность составит 99,7 %. Это означает, что на практике мы можем пренебречь шансами, что х окажется за пределами ![]() . Этот факт представляет собой важное правило нормального распределения, называемое правилом трех сигм. Оно служит основанием для определения контрольных пределов в контрольных картах.
. Этот факт представляет собой важное правило нормального распределения, называемое правилом трех сигм. Оно служит основанием для определения контрольных пределов в контрольных картах.
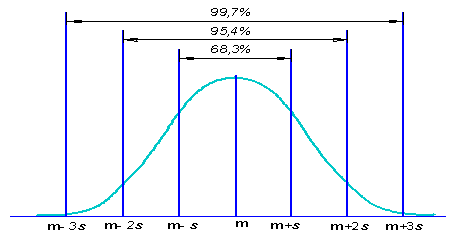
Рис. 3.17. Параметры m, ![]() и вероятности для нормального распределения
и вероятности для нормального распределения
Предпримем исследование воспроизводимости процесса. Оно важно при оценке того, сможет ли процесс пересечь границы поля допуска или нет. Если допустить, что процесс имеет нормальное распределение, то можно сразу же определить процент дефектных изделий, оказавшихся за данными границами допуска при данных параметрах (m, ![]() ). Но более полезно оценить процесс с помощью Ср — индекса воспроизводимости процесса. При двусторонних границах допуска
). Но более полезно оценить процесс с помощью Ср — индекса воспроизводимости процесса. При двусторонних границах допуска ![]() и
и ![]()
![]() ,(3.1)
,(3.1)
при односторонних границах допуска
![]() .
.
Оценка процесса с помощью Ср: 1) 1,33 * Ср — вполне удовлетворительно;
2) 1,00 * Ср < 1,33 — адекватно; 3) Ср < 1,00 — неадекватно /5/.