На практике часто важно изучить зависимости между парами соответствующих переменных. Как, например, установить, зависит ли вариация размеров детали от изменений скорости шпинделя токарного станка? Для изучения зависимостей между двумя переменными, такими, как скорость токарного станка и размер детали или концентрация и удельный вес, мы можем воспользоваться диаграммой рассеивания. Эти две переменные могут относиться:

а) к характеристике качества и влияющему на нее фактору;

б) двум различным характеристикам качества;

в) двум факторам, влияющим на одну характеристику качества.

Для установления связи между ними важно, прежде всего, построить диаграмму рассеивания и понять ситуацию в целом. Такие диаграммы строятся в следующей последовательности.

Этап 1. Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость, и расположите их в таблицу. Было бы хорошо иметь, по меньшей мере, 30 пар данных.

Этап 2. Найдите максимальные и минимальные значения и для х, и для y . Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей получились приблизительно одинаковыми, тогда диаграмму будет легче читать. Возьмите на каждой оси от 3 до 10 градаций и используйте для облегчения чтения круглые числа. Если одна переменная — фактор, а вторая — характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества — вертикальную ось у.

Этап 3. На отдельном листе бумаги начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.

Этап 4. Сделайте все необходимые обозначения. Убедитесь, что нижепере-численные данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто делал диаграмму: а) название диаграммы; б) интервал времени; в) число пар данных; г) названия и единицы измерения для каждой оси; д) данные оператора, который делал эту диаграмму.

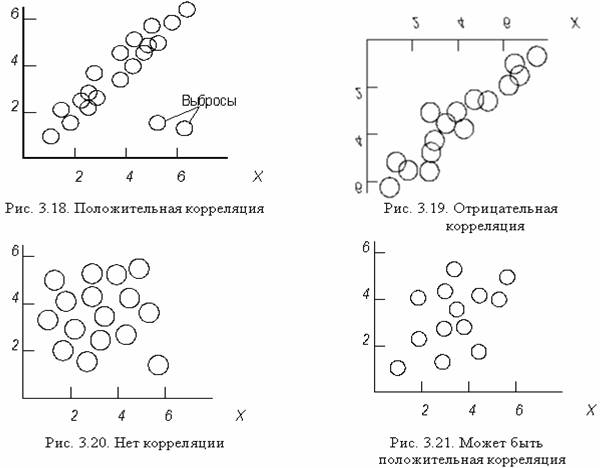
Точно так же, как по гистограмме можно распознать форму распределения, по диаграмме рассеивания можно представить себе общее распределение пар. Для этого вам сначала следует выяснить, есть ли на диаграмме какие-нибудь далеко отстоящие точки (выбросы). В общем, можно предположить, что любые такие точки, удаленные от основной группы (рис. 3.18), либо результат ошибок измерения или записи данных, либо обусловлены некоторыми изменениями в условиях работы. Эти точки надо обязательно исключить из корреляционного анализа. Однако вместо того, чтобы совершенно пренебречь этими точками, мы обратим внимание на причины таких нерегулярностей, поскольку, отыскивая их причины, мы получаем полезную информацию.

Возможны многочисленные варианты скоплений точек и некоторые, типичные из них приведены на рис. 3.18 – 3.21. На рис. 3.18 величина у растет с ростом х; это положительная корреляция. Причем на рис. 3.18 эта тенденция выражена очень ярко, и следует говорить о сильной положительной корреляции. На рис. 3.19 показана ситуация, обратная положительной корреляции, поскольку с ростом х величина у уменьшается; это отрицательная корреляция.  А на рис. 3.20 приведен случай, когда между х и y нет никакой определенной связи, так что здесь можно говорить об отсутствии корреляции.

Для изучения связи между х и y, прежде всего, важно нарисовать диаграмму рассеивания, но для установления силы связи в количественных показателях полезно вычислить коэффициент корреляции в соответствии со следующим определением:

,

где ;   ;   .

Здесь "n" — это число пар данных, а S(xy) называется ковариацией. Коэффициент корреляции (r) принимает значения из диапазона -1 < r < 1. Если абсолютное значение r окажется больше 1, то совершенно ясно, что произошла ошибка. В случае сильной положительной корреляции (см. рис. 3.18) достигается значение, близкое к +1, а при сильной отрицательной корреляции (см. рис. 3.19) достигается значение, близкое к –1. Таким образом, когда  близок к 1, это указывает на сильную корреляцию между x и y, а когда  близок к 0 – на слабую корреляцию.