Пусть прямые l 1 и l 2 заданы каноническими уравнениями:
l 1: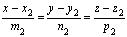 
l 2: 
.
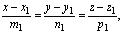Направляющие векторы этих прямых соответственно будут:
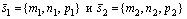
Углом между прямыми называется угол между прямыми, проведенными параллельно данным через какую-нибудь точку пространства. Один из смежных углов, очевидно, будет равен углу между направлявшими векторами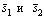
, который вычисляется по формуле (2.4):
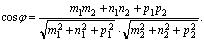
Условия параллельности и перпендикулярности прямых совпадают, соответственно с условиями параллельности или перпендикулярности векторов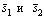.Чтобы определить взаимное расположение прямых l 1 и l 2 и найти точку их пересечения (если они пересекаются), достаточно решить систему уравнений с тремя неизвестными:
Если эта система имеет единственное решение х 0, у 0, z 0, то прямые пересекаются в точке М 0( х 0, у 0, z 0). Если система имеет бесконечное множество решений, то прямые совпадают.Если система не имеет решений, то прямые l 1 и l 2 не имеют общих точек, а потому либо параллельные, либо скрещивающиеся. Пусть заданы плоскость 
и прямая l
пересекаются; если система несовместна, то
; если система имеет бесконечное множество решений, то прямая l лежит в плоскости.Условие параллельности l и совпадает с условием перпендикулярности векторов
Условие перпендикулярности l и будет выглядеть так:
(Убедитесь в этом!).
Пример 3.7. Выяснить взаимное расположение прямой l и плоскости
, если они заданы уравнениями:
Решение. Запишем уравнения прямой l в параметрической форме:
(3.16)
1) Подставим эти выражения в уравнение плоскости
, получим:
.
Решая это уравнение, получим t 1 = 1. Подставим это значение в систему (3.16) получим
,
,
. Следовательно, прямая и плоскость пересекаются в точке М 1(3, 2, 7).2) Подставим х , у , z из (3.16) в уравнение плоскости
:
. 3) Подставим х , у , z из системы (3.16) в уравнение плоскости:
отсюда видно, что параметр t может принимать любые значения, при этом соответствующая точка прямой l принадлежит плоскости
. Значит, прямая l лежит в плоскости.