Предположим, что две монохроматические световые волны, накладываясь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления:

     .

Амплитуда результирующего колебания в данной точке удовлетворяет условию:

Так как волны когерентны, то имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому интенсивность результирующей волны (I ~ A²):

.

В точках пространства, где , интенсивность , там; где , интенсивность . Следовательно, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока.  Это значит, что в одних местах возникают максимумы, а в других –  минимумы интенсивности, т.е. усиление или ослабление интенсивности.  Это явление называется интерференцией света.

Разность фаз  некогерентных волн непрерывно изменяется, поэтому среднее во времени значение равно нулю, и интенсивность результирующей волны всюду одинакова и при  равна 2.

При использовании когерентных волн равной интенсивности в результате интерференции в максимумах  интенсивность равна ,  в минимумах I = 0).

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга и создают интерференционную картину.

Пусть разделение на две когерентные волны происходит в определенной точке О (рис.4.1). До точки М, в которой наблюдается интерференционная картина, одна волна в среде с показателем преломления п₁ прошла путь s₁, вторая –  в среде с показателем преломления п₂ –  путь s₂. Если в точке О фаза колебаний равна wt, то в точке М первая волна возбудит колебание, вторая волна – колебание , где  – соответственно фазовые скорости первой и второй волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна:

,

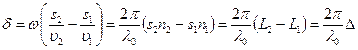где  – длина волны в вакууме. Произведение геометрической длины (s) пути световой волны в данной среде на показатель (п) преломления этой среды называется оптической длиной пути (L), а  – разность оптических длин проходимых волнами путей – называется оптической разностью хода.

Если оптическая разность хода равна целому числу волн в вакууме:

 ,            где            (m = 0,1,2…),                  (4.2)

то и колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно, (3.2) является условием интерференционного максимума.

Если оптическая разность хода равна нечетному числу длин полуволн:

,       где      (m = 0,1,2…),                  (4.3)

то  и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе, т.е. будут гасить друг друга. Следовательно, (4.3) является условием интерференционного минимума.