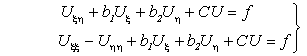Введем обозначения (для сокращения и удобства письма):
.
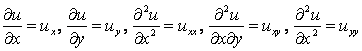Пусть дано уравнение
, (4.1)
где 
– заданные функции х, y.
Это уравнение называется линейным. Если 
, то уравнение называется линейным однородным, в противном случае линейным неоднородным. Если все коэффициенты постоянные, то уравнение называется линейным уравнением с постоянными коэффициентами.
Практика и теория подтверждает, что с помощью преобразования переменных 
данное дифференциальное уравнение остается линейным:
, (4.2)
где коэффициенты [7]:
Спрашивается: нельзя ли выбрать переменные 
и 
так, чтобы в преобразованном уравнении (4.2) некоторые коэффициенты обратились в нуль? Эта возникшая задача связана с решением обыкновенного дифференциального уравнения, которое называется характеристическим для исходного с частными производными:
(4.3.)
Его интегралы называются характеристиками.
Если 
– общий интеграл (4.3), то, положив 
, мы обратим в нуль коэффициент 
при 
.
Если 
– другой интеграл (4.3), линейно независим от 
, то полагают 
, тем самым в нуль обращают 
при 
.
Уравнение (4.3.) можно записать так:
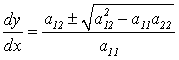. (4.4)
Если 
, то 
и 
– действительные и различные. Делая замену, приводим уравнение к виду:
(4.5)
В этом случае говорят, что уравнение имеет гиперболический тип. Если положить 
, 
, то уравнение примет вид:
. (4.6)
Если 
, то имеем один общий интеграл 
. Пусть 
– любая функция, линейно независимая от 
, тогда: 
, и исходное уравнение будет иметь вид:
(4.7)
В этом случае говорят, что уравнение имеет параболический тип.
Если 
, то характеристическое уравнение имеет комплексно сопряженные интегралы:
и 
,
и, положив 
уравнение приведем к виду:
, (4.8)
который называется эллиптическим.
Если коэффициенты линейного уравнения постоянные, то характеристическое уравнение имеет решение:
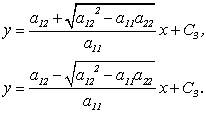
При 
уравнение приводится к виду:
|
или |
|
, |
который называется гиперболическим.
При 
уравнение приводится к параболическому типу:
При 
уравнение приводится к эллиптическому типу:
Пример 1
Привести к каноническому виду уравнение: 
Решение. Запишем, чему равны для нашего случая коэффициенты. Так как: 
имеем уравнение параболического типа.
Характеристическое уравнение имеет вид:
Решая его, находим, что общий интеграл x – y = C.
Положим 
, а в качестве другой переменной возьмем 
. При этом: 
Тогда
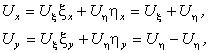
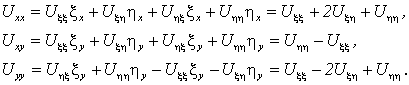
Подставляя значения частных производных в исходное уравнение, после простых преобразований получим:
.
Пример 2
Привести к каноническому виду уравнение:
Решение. 
т.е. имеем уравнение эллиптического типа. Составим уравнение характеристик: 
или 
.
Отсюда 
; получаем два семейства комплексно сопряженных характеристик:
и 
.
Делаем замену переменных: 
;
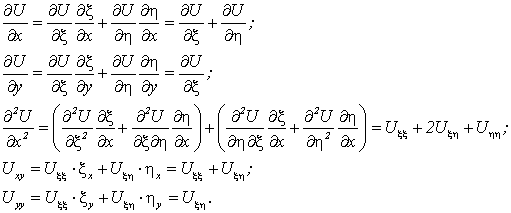
Подставив эти значения в исходное уравнение, получим
Пример 3
Привести к каноническому виду уравнение: 
Решение. Здесь 
– уравнение гиперболического типа. Уравнение характеристик:
.
Отсюда
и 
.
Проинтегрировав эти уравнения, получим два семейства характеристик:
и 
.
Отсюда
и 
т.е. получили уравнения характеристик. Вводим новые переменные: 
. Далее необходимо выразить частные производные по старым переменным через новые (требуется использовать правило дифференцирования сложной функции двух независимых переменных):
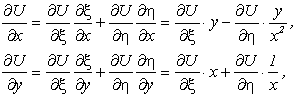
далее рекомендуется найти производные второго порядка самостоятельно в качестве упражнений и получить окончательный результат:
.
Получили уравнение канонического вида.