Если тепловые источники  отсутствуют, то температура   однородного стержня удовлетворяет уравнению теплопроводности (4.44).

Будем полагать, что задан режим (начальное условие) (4.35). Предположим также, что концы стержня  и  имеют температуру, равную нулю (говорят, что это температура внешней среды), т.е. имеем простейшие краевые условия (4.35) при любом .

Для уравнения (4.44) сначала будем искать ненулевые решения вида:

,                                                  (4.46)

где, как и ранее,  – функция одной переменной , а  – переменного . Так как

то, подставив эти значения производных в уравнение (4.44.), получим:

.

Отсюда, разделив переменные, будем иметь:

                                                                                                      (4.47)

(знак «минус» взят, потому что другие значения не дадут нужных решений). Получаем из (4.47) два обыкновенных дифференциальных уравнения:

,    .                                          (4.48)

Первое уравнение имеет общее решение:

,                                              (4.49)

где  и  – произвольные постоянные.

Второе уравнение дает общее решение:

,

где  – произвольная постоянная. Перемножая функции , получим:

                                     (4.50)

где . Функции (4.50), при любом виде  удовлетворяют уравнению (4.44). Потребуем, чтобы они удовлетворяли также краевым условиям (4.35). Положим , получим , отсюда . Следовательно,

.                                                     (4.51)

Но , ибо имели бы нулевое решение.

Положим , в силу условия (4.35) будем иметь:

 .

Но  , ибо тогда . Поэтому , откуда находим  или . Эти числа называются характеристическими числами задачи, а совокупность их  спектром задачи. Каждому  соответствует частное решение уравнения теплопроводности:

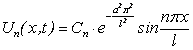.                                            (4.52)

Замечание. В качестве п достаточно брать лишь целые положительные числа (n = 1,2,…), так как при п = 0 имеем , что противопоказано, а при п < 0 получаем решения той же природы.

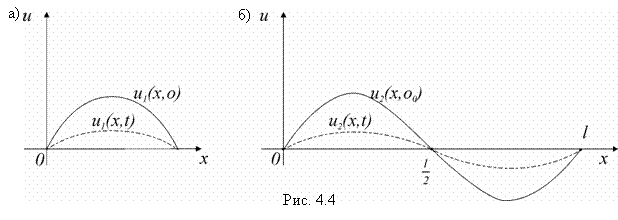
Итак, формула (4.52) дает полный набор линейно независимых частных решений вида (4.46) уравнения теплопроводности (4.44), удовлетворяющих граничным условиям (4.35). Физически функции  представляет собой температурные волны, графиками которых являются затухающие при  синусоиды (рис. 4.4).

Осталось удовлетворить начальное условие (4.35). Так как уравнение исходное (4.44) линейное, однородное, то можно применить принцип наложения решений. Отсюда будем иметь:

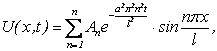                                        (4.53)

причем, если ряд (4.53) сходится, то при известных условиях этот ряд  есть решение уравнения (4.44). При t  = 0   в силу начального условия (4.35) получаем:

.                                                (4.54)

Ряд (4.54) есть ряд Фурье для  по синусам.

Коэффициенты вычисляются по формуле:

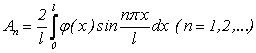                                 (4.55)

Вывод: решение задачи имеет вид (4.53), коэффициенты которого находятся по формулам (4.55). Для обычной инженерной практики достаточно брать несколько членов ряда. Примененный метод, как и ранее, носит название метода разделения переменных Фурье.

Из (4.53) следует, что . Физический смысл этого соотношения ясен: все тепло из стержня вытечет и в нем установится температура нулевая (например, льда, если концы погрузить в него).

Перейдем к задаче второго режима, а именно когда концы стержня теплоизолированы (4.45):

.

Для этой задачи вспомогательная задача состоит в нахождении функции: , удовлетворяющей уравнению (4.44) и условиям (4.45). Эти условия дают:

.                                                         (4.56)

Подстановка  в (4.44) снова приводит к формуле:

,                                                        (4.57)

где . Случай  исключается. Но  уже возможно. Оно дает , откуда , . Согласно (I.6.11)  и поэтому Х=С, С – произвольная постоянная. Кроме того, при  уравнение (I.6.12) дает , т.е. , где .

Значит, одним из решений вспомогательной задачи будет:

.                                                            (4.58)

Пусть . Это дает  и , но тогда , и первое из соотношений (4.56) дает , так что (после замены С₁ на С) Х примет вид:

.

Отсюда и из второго условия (4.56), получаем:

.

Следовательно,              и .

Итак,                               .

Подставляя в (4.57) одно из найденных значений , находим:

Отсюда

.

Полагая , имеем бесчисленное множество функций:

,

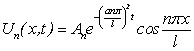удовлетворяющих (4.44) и (4.45). Тогда

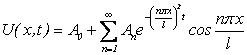                                        (4.59)

будет решением (4.44), удовлетворяющим (4.45).

Остается подобрать  так, чтобы получить , т.е.

.

Для чего надо взять

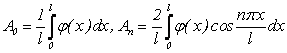.                               (4.60)

Пример 1

Найти решение уравнения теплопроводности:

при граничном условии  и начальном условии:

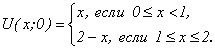
Решение. В нашем случае решение определяется по формуле (4.53.); где а = 1;  l = 2:

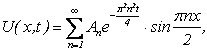
где        вычисляется по формуле:

.

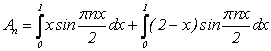Вычисляя интегралы, получим:

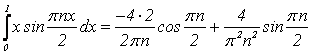
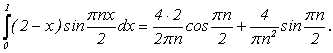
Складывая значения интегралов, получим:

.

Так как , то ; .

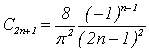Решение задачи будет:

.

Пример 2

Один конец стержня  х = 0  теплоизолирован, а другой  x = l  поддерживается при температуре U(l, t) = 0.  В начальный момент времени  t = 0  температура всех точек стержня равна U₀. Найти распределение температуры при  t > 0.

Решение. Задача сводится к решению уравнения:

удовлетворяющего начальному условию U(x, 0) = U₀ и граничным условиям , и  (условие теплоизоляции конца  х = 0  означает, что ).

Применяя метод Фурье, найдем, что уравнение (4.44) имеет решение:

.

Из граничных условий получим:

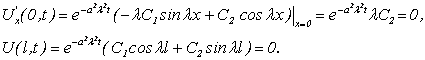
Из первого уравнения следует, что  ибо  (получили бы нулевое решение), из второго уравнения следует, что . Решая второе уравнение, получим: . В результате имеем бесчисленное множество решений:

,

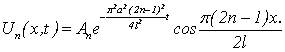удовлетворяющих граничным условиям.

Решение задачи ищем в виде ряда:

Из начального условия получим:

Эта формула позволит найти . Для этого разложим в ряд Фурье четную функцию, имеющую период 4l и равную  при   –l < x < l,   но при 

.

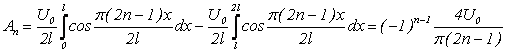Окончательное решение задачи имеет вид:

.