1). Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (например, свободный электрон в металле или электрон в атоме). Такая «яма» описывается потенциальной энергией вида:

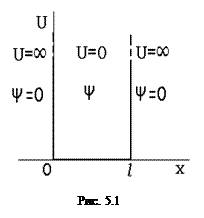
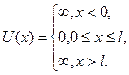
где l – ширина «ямы», а энергия отсчитывается от ее дна (рис 5.1) .

Уравнение Шредингера в этом случае имеет вид (для области внутри «ямы»):

,

и имеет решение при собственных значениях энергии:

,

где n = 1, 2, 3… – главные квантовые числа. Следовательно, энергия частицы в «потенциальной яме» принимает дискретные значения, т.е. квантуется. Отметим, что классическая механика никаких ограничений на энергию не накладывает. Квантованные значения энергии (Е_n) называются уровнями энергии. Собственные значения функции в данной задаче имеют вид:

.

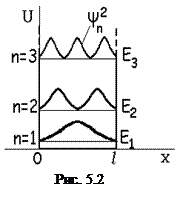
На рис. 5.2 изображены графики квадрата собственных функций соответствующие определенным уровням энергии.

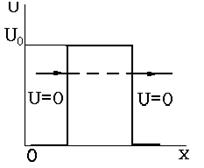
2). Туннельный эффект. Это чисто квантовое явление, когда частица проникает за потенциальный барьер, который классическая частица преодолеть не может. Потенциальный барьер представляет область пространства, в которой потенциальная энергия имеет вид, изображенный на рис. 5.3 (одномерный случай). Решение уравнения Шредингера для такого потенциала дает значения Y-функции, отличные от нуля и в области за потенциальным барьером. Значит, существует вероятность попадания частицы за потенциальный барьер, это похоже на то, что в потенциальном барьере для квантовой частицы имеется туннель. Примерами этого эффекта могут служить a-распад ядер, явление в контактном слое на границе двух полупроводников.

3). Одномерный гармонический осциллятор с потенциалом

,

где w – собственная частота колебаний осциллятора, имеет решения уравнения Шредингера при собственных значениях энергии:

,     n = 1, 2, 3,…

Формула показывает, что энергия квантового осциллятора также квантуется. Минимальная энергия называется энергией нулевых колебаний, является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.

Таким образом, даже при температуре Т = 0 энергия колебательного движения атомов отлична от нуля. Это подтверждается экспериментами по  рассеянию света кристаллами при Т® 0.