Место и задачи. Завершающим этапом моделирования опасных процессов в техносфере служит оценка интересующих нас их числовых параметров. Как правило, она связана с определением вероятности или частоты появления конкретных головных событий (катастроф, аварий, несчастных случаев), а иногда и математического ожидания их количества на заданном интервале времени. В большинстве случаев, однако, на данном этапе также рассчитываются размеры ущерба и затрат, связанных с возникновением и предупреждением происшествий на производстве и транспорте.
Поскольку конечная цель моделирования направлена не на оценку, а на обеспечение требуемой безопасности, то результаты количественного анализа исследуемых нами процессов нужны в первую очередь для обоснования соответствующих мероприятий. Вот почему при их выборе должны использоваться данные качественного анализа дерева происшествия — прежде всего выявленные в нем минимальные сочетания исходных предпосылок и оценки их значимости. Дело в том, что устранение причинных цепей, состоящих из наиболее значимых предпосылок, является самым легким и дешевым способом обеспечения заданного уровня безопасности.
Однако в ряде случаев отдельный интерес может представлять и автономная предварительная оценка числовых характеристик как головного события дерева происшествия, так и центрального события дерева их исходов, например, если нужно отдать предпочтение или принять обоснованное решение: а) о соответствии техногенного риска вновь созданного производственного или перевозочного процесса тому его значению, которое предъявлено техническим заданием; б) о выборе (по наименьшей вероятности происшествий) одного из нескольких, подготовленных на конкурсной основе однотипных технических проектов.
Укажем рекомендации, пригодные для последовательного проведения необходимой в таких случаях количественной оценки параметров каждой рассматриваемой нами диаграммы — вначале для дерева происшествия, а затем и для дерева событий — его возможных разрушительных исходов.
Формализация дерева происшествия. Подготовительным этапом к количественному анализу служит дальнейшая формализация рассматриваемой семантической диаграммы — аналитическое представление заданного ею процесса так называемой структурной функцией. В такой аналитической модели, помимо событий и связей между элементами, в качестве исходных данных также используются
параметры, характеризующие вероятность или частоту исходных предпосылок на конкретном интервале времени.
Например, для изображенного выше (см. рис. 5.2) дерева данная функция, увязывающая с помощью алгебры событий моделируемое головное событие с его промежуточными и исходными предпосылками, имеет следующий вид:
L = H×I×K = (A+B)(C+D)(E+F+G),
а в случае использования вероятности Q(L) в качестве объективной количественной меры появления происшествия, аналитическая формула для нее оказывается такой:
Q(L)=P(H)×P(I)×P(K)=P(A+B)·P(C+D)·P(E+F+G),
где P(А),…Р(К) – вероятности появления его событий — предпосылок.
Преобразование и упрощение структурных функций при необходимости осуществляют с соблюдением правил булевой алгебры. В частности, следуя закону поглощения, получают такие равенства:
A·(A·B) = A·B; A+(A+B) = A.
Общая последовательность анализа. При известных структурных функциях количественный анализ дерева происшествия и оценку вероятности достижения его головного события рекомендуется осуществлять в таком порядке: 1) аналитическая модель данного процесса декомпозируется на отдельные блоки – сомножители и слагаемые функции; 2) в выбранных блоках выделяются те подмножества событий, которые соединены между собой условиями "и", "или" и имеют известные вероятности появления; 3) проводится расчет вероятностей наступления вершинных для таких блоков событий; 4) структурная функция упрощается путем замены каждого подмножества одним членом, обладающим эквивалентной вероятностью; 5) подобным образом рассчитывается и вероятность появления головного события модели.
Правила расчета параметров. В процессе оценки числовых характеристик декомпозированного дерева происшествия следует руководствоваться рядом правил:
1) Объединенные логическим условием "и" n предпосылок заменяют одним событием с вероятностью появления PК (конъюнкция – Ù):
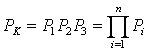
2) Соединенные логическим условием "или" m предпосылок заменяют одним событием c вероятностью PД (дизъюнкция – Ú):
![]()
которое при m = 2 и m = 3, рассчитывается по таким зависимостям:
P|m=2 = P1+P2-P1P2; P|m=3 = Р1+Р2+Р3-P1P2-P1P3-P2P3+P1P2P3.
3) При известных структурных схемах безотказности техники параллельно соединенные элементы соответствуют логическому условию "и" этого дерева, а последовательно соединенные – "или".
4) В случае объединения логическим условием "и" нескольких событий, одно из которых имеет близкую к единице вероятность, а другие – меньшую 0,01, допускается упрощение данной ветви путем отбрасывания события с большой вероятностью возникновения.
5) При объединении логическим условием "или" нескольких событий, одно из которых имеет близкую к нулю вероятность, а другие – на два-три порядка больше,
также можно упрощать соответствующую ветвь, но отбрасывать нужно событие с малой вероятностью.
6) Количественная оценка вероятности головного события может быть проведена также с помощью минимальных сочетаний событий – путем построения нового, эквивалентного исходному дерева, включающего в себя сочетания какого-либо одного типа. Однотипные сочетания соединяются в новом дереве всего одним логическим условием: "или" – для дерева, состоящего из одних МПС, и условием "и" – для дерева из МОС.
Например, если в анализируемом дереве происшествия число МПС равно a, в каждом i-м из которых содержится mi исходных событий-предпосылок, то можно построить новое дерево (рис. 5.3, а), включающее в себя a исходных (промежуточных для прежнего дерева) предпосылок, объединенных логическим условием "или". При этом в каждом из этих новых событий исходные предпосылки прежнего дерева должны быть соединены условием "и".
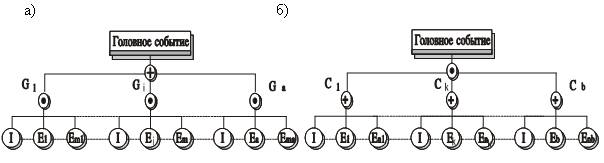
Рис. 5.3. Модификация дерева происшествий: а – первое, i-е и а-е МПС; б – первое, k-е и b-е МОС
Если же дерево происшествия содержит в себе b штук МОС с nk исходными предпосылками в каждом из них, то в новом дереве (рис. 5.3, б) исходные события следует объединять логическим условием "и", а каждую предпосылку этой упрощенной модели образовывать логическим сложением исходных событий дерева-оригинала. Отсюда следует, что для расчета вероятности возникновения происшествий Q могут быть использованы следующие выражения:
![]()
![]()
где a, b – количество соответственно минимальных пропускных и минимальных отсечных сочетаний дерева происшествия;
mi, nk – число исходных предпосылок в каждом его i-м пропускном и k-м отсечном минимальных сочетаниях исходных событий-предпосылок.
Прогноз при нечетко заданных исходных данных. При отсутствии достоверных данных о количественных параметрах исходных предпосылок, приближенную оценку возможности появления происшествий следует проводить с помощью нечетких чисел, которые задаются отрезками с одним, наиболее возможным – m и двумя предельными их значениями: наименьшим – (m-a) и наибольшим – (m+b).
Легче всего прогноз меры возможности появления головного события ![]() образуемого логическим сложением или перемножением n предпосылок,
образуемого логическим сложением или перемножением n предпосылок,
проводить после предварительной аппроксимации их параметров нечеткими числами (m,a, b) в форме L-R /12/.
Обозначая приближенные параметры предпосылок через ![]() , можно рассчитать нечеткую меру возможности появления результирующих событий, образуемых логическим условием "и":
, можно рассчитать нечеткую меру возможности появления результирующих событий, образуемых логическим условием "и":
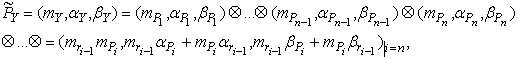
где Ä – операция перемножения нечетких чисел в L-R форме;
![]() – рекурсивные члены, рассчитываемые по формулам
– рекурсивные члены, рассчитываемые по формулам
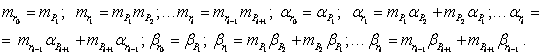
Подобно проводится приближенная оценка возможности появления события, образованного в дереве логическим условием "или":
![]() где
где ![]() – аналогичные члены, рассчитываемые по формулам:
– аналогичные члены, рассчитываемые по формулам:
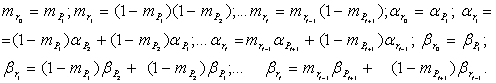
Наиболее подходящей областью применения нечеткого интервального метода прогнозирования происшествий является оценка возможности появления и предупреждения уникальных (редких и наиболее тяжелых по последствиям) катастроф и аварий. В этом случае оправданы необходимость привлечения высококвалифицированных экспертов и повышенная трудоемкость моделирования, что связано с проведением итерационных процедур вычисления.
Отметим также, что как приближенные, так и точные количественные параметры исходных событий-предпосылок дерева происшествия следует определять на основе проектных или статистических данных по интенсивности отказов техники, частоте возникновения ошибок эксплуатирующего ее персонала и вероятности нерасчетных для них внешних воздействий.
Эти показатели могут быть найдены в соответствующей научно-технической литературе. При выборе необходимых исходных данных необходимо учитывать как условия расположения и эксплуатации техники, так и психофизиологическое состояние работающего на ней персонала.
Особенности анализа дерева исходов. В завершение данного параграфа и главы в целом дадим рекомендации, касающиеся особенностей количественного анализа дерева событий – исходов происшествия. Прежде всего отметим, что его целью служит не только предварительная количественная оценка ожидаемого среднего социально-экономического ущерба, но и обоснование наиболее эффективных мероприятий по его снижению в случае необходимости.
Решение каждой из этих главных задач может быть осуществлено лишь с использованием трех уровней соответствующей семантической модели – путем последовательного определения: а) количества нежелательно высвободившихся энергии или вещества – К=М, б) размеров пространства, в пределах которого сформировались поля поражающих факторов таких выбросов или продуктов их
последующей трансформации – П, в) величины ущерба от их разрушительного воздействия на оказавшиеся в зонах поражения этих факторов людские, материальные и природные ресурсы – Y.
Общая последовательность. Порядок расчета перечисленных выше показателей совместно с условиями контроля правильности необходимых исходных данных проиллюстрирован на рис. 5.4. Расположенная непосредственно под "деревом" строка нижней таблицы содержит формулы, необходимые для последовательного прогноза количества аварийно высвободившихся энергии или вредного вещества – К=М, размеров поражаемой ими площади – П и величины причиненного ущерба – Y. Они рассчитываются на каждом уровне этой модели как математические ожидания соответствующих случайных величин – M[K], M[П] и M[Y].
В самой нижней строке рис.5.4 приведены критерии проверки правильности исходных данных об условных вероятностях, используемых при количественном анализе данной семантической модели. В частности, в данном случае сумма всех условных вероятностей каждого уровня дерева должна быть равной точно Q, а не единице, как это имело место при проверке полноты его возможных исходов, где они рассматривались как составляющие полную группу независимых событий – см. формулу (5.1).
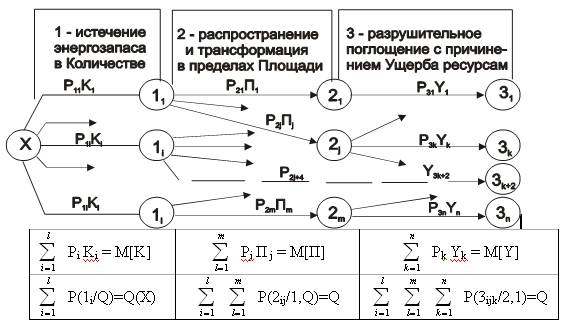
Рис. 5.4. Порядок и условия расчета ожидаемого ущерба
Показанное в центральной части рис. 5.4 дерево учитывает не все, а лишь наиболее характерные последовательности образующих его промежуточных и конечных событий. Это символизируется оборванными ветвями, заканчивающимися стрелками, и штриховым обозначением ветви, соединяющей события 1i и 3k+2. Она учитывает возможность объединения двух уровней модели, например, распространения и поглощения электрической энергии телом человека, включенного в соответствующую цепь: в данном случае прохождение электрического тока одновременно сопровождается его частичным поглощением с губительными для здоровья последствиями.
Исходные данные. Естественно, что количественный прогноз техногенного риска с помощью дерева событий требует информации о всех параметрах модели,
изображенной на рис. 5.4. Напомним, что состав учитываемых ею основных факторов (свойств человеко-машинных систем) приведен в конце предыдущего параграфа.
Укажем также, что детальные рекомендации, касающиеся порядка прогнозирования средних объемов – М[К], площадей – M[П] и ущербов – M[Y], будут приведены в заключительной главе. В этом параграфе мы ограничимся рассмотрением лишь способов предварительной оценки количества вредного вещества, высвободившегося в результате происшествий, связанных с разгерметизацией соответствующих резервуаров.
Прогноз количества выброшенного вещества. При оценке объема аварийной утечки химически вредных и взрывоопасных веществ, находящихся в газообразном или жидком состоянии, для каждого такого случая нужно рассматривать по два сценария /8, 13/:
1) высвобождение всего их объема по причине полного разрушения сосуда,
2) частичное опустошение емкости или магистрали вследствие нарушения их герметичности.
В первом случае, например, количество высвободившегося газообразного вредного вещества равно всей его массе G, а если она неизвестна, то рассчитывается по такой формуле:
К = (m /R)×VP/R(T+273,15), (5.2)
где m – молярная масса вредного вещества, кг/моль; R – универсальная газовая по-стоянная, равная 8,31 Дж/(кг/моль); V – его объем, м3, P – давление, Па; T – температура, °С.
Подобным, но более громоздким способом определяется и объем пролитого жидкого вещества. Последнее связано с необходимостью учета части вредного вещества, частично находящегося в газообразной фазе, а затем и его испарения в момент и после аварийного высвобождения жидкости из емкости.
Во втором случае, интенсивность высвобождения газообразного вредного вещества по причине частичной разгерметизации емкости – q, кг/с, следует оценивать по наименьшему значению правой части следующей формулы:
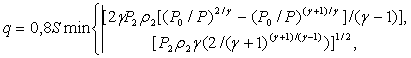 (5.3)
(5.3)
где S – площадь отверстия разгерметизации емкости, м2;
P, P0 – давления внутри и за пределами емкости, Па;
r2, g – соответственно плотность вредного вещества, кг/м3 и значение показателя его адиабаты.
При известной массе вредного вещества в емкости М, кг, продолжительность истечения t, с, должна рассчитываться делением М на q, а при отсутствии этой информации, таким образом:
t = (m /R)×VP/[R(T+273,15)q. (5.4)
Предполагается, что все параметры, входящие в формулы (5.2) – (5.4), могут быть найдены в конструкторско-технологической документации на конкретное производственное или транспортное оборудование либо оценены с помощью имеющихся статистических данных (аналогов).
Оценка эффективности альтернатив. Остановимся на рекомендациях, касающихся порядка обоснования мероприятий по снижению техногенного риска с помощью диаграмм причинно-следственных связей типа "дерево". Необходимость в этом всегда возникает в тех случаях, когда априорная оценка величины техногенного
риска приводит к результатам, не удовлетворяющим требованиям к безопасности проведения производственных или перевозочных процессов. Например, ожидаемые вероятности возникновения происшествий или ущерб от них превышают максимально допустимые значения, что требует принятия мер по снижению соответствующего риска.
Выходом из создавшихся ситуаций может быть внедрение дополнительных организационно-технических мероприятий, направленных на предупреждение происшествий либо на снижение ущерба от них в случае появления. Очевидно также, что каждое организационное мероприятие и техническое средство потребуют для своего использования затрат, не обязательно пропорциональных ожидаемой от них эффективности. В этих условиях целесообразна оптимизация либо по критерию минимума затрат на внедрение дополнительных мероприятий, либо по максимуму снижения вероятности появления рассматриваемых нами катастроф, аварий и несчастных случаев с людьми.
Решение задачи по обоснованию оптимальных мероприятий может быть осуществлено лишь с помощью рассматриваемых нами моделей типа "дерево". Для определения эффекта, ожидаемого от внедрения конкретного технического средства или организационного мероприятия, необходимо провести расчет при новых (уменьшенных) значениях вероятностей появления связанных с ними предпосылок дерева происшествий или вариантов разрушительного высвобождения и воздействия потоков энергии и вещества.
Критерии оценки эффективности. Очевидно, что самыми предпочтительными будут те мероприятия, которые соответствуют: а) наибольшему (при заданных затратах) снижению либо вероятности головного события дерева происшествия, либо среднего ущерба от вызванных им наиболее разрушительных вариантов высвобождения энергозапаса; б) наименьшим затратам на внедрение мероприятий с целью получения требуемого от них эффекта (снижения техногенного риска до приемлемого уровня).
Напомним, что выбор подобных мероприятий лучше всего проводить с учетом значимости или критичности соответствующих событий-предпосылок дерева происшествия.
Принципы оптимизации альтернатив. При формулировании данных принципов мы исходили из того, что на практике одновременно приходится иметь дело с несколькими организационно-техническими мероприятиями и большим количеством образуемых ими альтернативных сочетаний.
Например, даже для двух мероприятий возможны уже четыре альтернативы: внедрить первое, второе, оба вместе или отказаться от них. Это предполагает необходимость достаточно трудоемкого перебора, трудно реализуемого без использования современных математических и машинных методов.
К сожалению, не представляется возможным детально рассмотреть такие методы в данной работе. Укажем лишь, что подробную математическую постановку данной оптимизационной задачи и способы ее решения можно найти, например, в монографии /14/. В качестве метода ее решения там рекомендуется динамическое программирование, а исходными данными служат: ожидаемые вероятность Q(X) или риск ущерба от происшествий M[Y], величина затрат, выделенных для совершенствования безопасности SВ, а также сопутствующие каждой альтернативе затраты Si и ожидаемый от них эффект: DPi ®DQi(X)®DMi[Y].
Естественно, что самым лучшим, а в ряде случаев и единственно возможным, методом предварительной оценки трех последних параметров является моделирование происшествий, в том числе и с помощью рассмотренных выше диаграмм типа "дерево".
Данный факт еще раз подтверждает актуальность и плодотворность рассмотренных здесь методов моделирования опасных производственных и транспортных процессов, а также необходимость в дополнительных рекомендациях, касающихся прогнозирования сопутствующего им ущерба.
Контрольные вопросы
1. Для чего используются модели диаграмм типа «дерево»?
2. Особенности построения модели «дерево происшествий».
3. Особенности построения модели «дерево исходов».
4. Что такое минимальное пропускное сочетание?
5. Что такое минимальное отсечное сочетание?
6. В чем суть количественного анализа моделей типа «дерево»?