Одним из примеров применения моделей оптимизации может служить задача оптимизации периода стойкости металлорежущего инструмента. В данном случае целевой функцией является суммарный период стойкости инструмента (![]() ), являющийся функцией геометрических параметров инструмента, элементов режима резания и периода стойкости между переточками. Задача заключается в определении величин технологических параметров, например, периода стойкости между переточками (
), являющийся функцией геометрических параметров инструмента, элементов режима резания и периода стойкости между переточками. Задача заключается в определении величин технологических параметров, например, периода стойкости между переточками (![]() ), доставляющих максимум целевой функции при наложении на величины входных параметров ограничений, определяемых их физической природой. На рис. 5.1 приведена схема износа режущего инструмента и типовая кривая износа при износе инструмента по передней и задней поверхности.
), доставляющих максимум целевой функции при наложении на величины входных параметров ограничений, определяемых их физической природой. На рис. 5.1 приведена схема износа режущего инструмента и типовая кривая износа при износе инструмента по передней и задней поверхности.
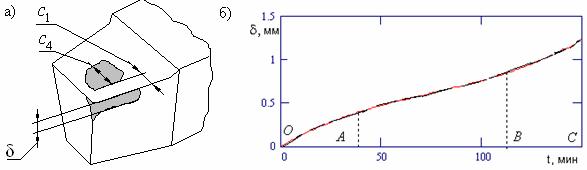
Рис. 5.1 Схема износа металлорежущего инструмента вдоль лезвий (а) и общий
вид кривой износа (б): ВС – период катастрофического износа; АВ – период стабильной работы; ОА – период приработки
Задача оптимизации суммарного периода стойкости заключается в определении оптимального износа по задней поверхности ![]() и соответствующего ему периода стойкости
и соответствующего ему периода стойкости ![]() . Введем понятие оптимального износа.
. Введем понятие оптимального износа.
Оптимальный износ – величина линейного износа задней поверхности металлорежущего инструмента, при использовании которой в качестве критерия износа суммарный период стойкости инструмента достигает максимальной величины.
Суммарный период стойкости любого конкретного инструмента является функцией периода стойкости между переточками (рис. 5.2) и определяется следующим образом:
![]() , (5.1)
, (5.1)
где ![]() – период стойкости (время резания инструментом между переточками);
– период стойкости (время резания инструментом между переточками); ![]() – число переточек.
– число переточек.
В большинстве случаях вместо формулы (5.1) может быть использована приближенная формула, несколько упрощающая дальнейшие вычисления
![]() (5.2)
(5.2)
Число переточек ![]() , в свою очередь, также является функцией геометрических параметров инструмента и величины износа по задней поверхности
, в свою очередь, также является функцией геометрических параметров инструмента и величины износа по задней поверхности ![]() , которая используется в качестве критерия износа. На рис. 5.Ошибка! Закладка не определена. изображена режущая часть резца или другого инструмента с линейным износом
, которая используется в качестве критерия износа. На рис. 5.Ошибка! Закладка не определена. изображена режущая часть резца или другого инструмента с линейным износом ![]() . Чтобы инструмент стал вновь работоспособным, с задней поверхности при переточке должен быть сошлифован слой твердого сплава толщиной
. Чтобы инструмент стал вновь работоспособным, с задней поверхности при переточке должен быть сошлифован слой твердого сплава толщиной ![]() . Толщина слоя определяется следующим образом:
. Толщина слоя определяется следующим образом:
![]() . (5.3)
. (5.3)
Введем обозначения ![]() ,
,
тогда
![]() .
.

Рис. 5.2 Кривая износа режущего инструмента (f) ![]() и график
и график
зависимости ![]() (б)
(б)
Дополнительный слой ![]() включает допуск на заточку и слой твердого сплава, сошлифовываемый для удаления дефектов, образовывающихся под изношенной частью задней поверхности.
включает допуск на заточку и слой твердого сплава, сошлифовываемый для удаления дефектов, образовывающихся под изношенной частью задней поверхности.
Размер ![]() (рис. 5.3), измеряемый по передней поверхности, называется допустимой величиной стачивания. Его величина обусловливается конструкцией инструмента. Тогда размер
(рис. 5.3), измеряемый по передней поверхности, называется допустимой величиной стачивания. Его величина обусловливается конструкцией инструмента. Тогда размер ![]() слоя инструментального материала, перпендикулярный задней поверхности и соответствующий допустимой величине стачивания, равен:
слоя инструментального материала, перпендикулярный задней поверхности и соответствующий допустимой величине стачивания, равен:
![]() .
.
В этом случае суммарный период стойкости в форме (5.2) выразится следующей формулой:
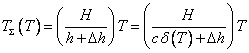 , (5.4)
, (5.4)
или
![]() . (5.5)
. (5.5)
Тогда математическая модель оптимизации в виде (3.2) будет выглядеть следующим образом:
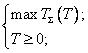 или
или 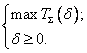 (5.4)
(5.4)
где ![]() и
и ![]() выражаются из формул (5.4) и (5.5) соответственно.
выражаются из формул (5.4) и (5.5) соответственно.
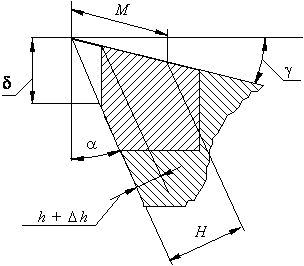
Рис. 5.3 Схема к построению математической модели оптимизации ![]()
Для решения данной математической модели может быть использован любой из рассмотренных нами методов оптимизации. Так, например, при решении с использованием необходимых и достаточных условий экстремума и зависимости (5.5), требуется определить корни уравнения:
![]() . (5.7)
. (5.7)
Так как период стойкости является функцией износа, ![]() , то его производная будет равна:
, то его производная будет равна:
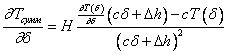 . (5.8)
. (5.8)
Для дальнейшего аналитического решения необходимо знать вид и коэффициенты зависимости ![]() . Зависимость, представленная кривой износа (см. рис. 5.1 и 5.2), может быть описана полиномом третьей степени вида:
. Зависимость, представленная кривой износа (см. рис. 5.1 и 5.2), может быть описана полиномом третьей степени вида:
![]() , (5.9)
, (5.9)
При использовании в качестве эмпирической зависимости полинома в форме (5.9) решение задачи оптимизации приводит к поиску корней уравнения
![]() , (5.10)
, (5.10)
В случае если ![]() > 0, уравнение (5.10) имеет единственное решение в вещественной области. В случае если
> 0, уравнение (5.10) имеет единственное решение в вещественной области. В случае если ![]() принимается равным нулю, уравнение имеет два вещественных корня, один из которых равен нулю и, следовательно, находится вне области допустимых решений. Графики на рисунке 5.4 иллюстрируют нахождение корней уравнения (5.10).
принимается равным нулю, уравнение имеет два вещественных корня, один из которых равен нулю и, следовательно, находится вне области допустимых решений. Графики на рисунке 5.4 иллюстрируют нахождение корней уравнения (5.10).
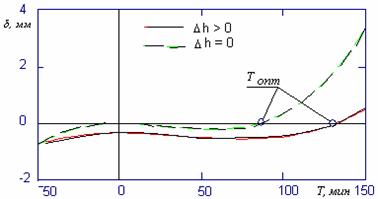
Рис. 5.4 Схема к определению корней уравнения ![]()
Очевидно, значения ![]() , найденные аналитически, должны быть приведены к ближайшему значению
, найденные аналитически, должны быть приведены к ближайшему значению ![]() , кратному машинному времени и обеспечивающему большее значение
, кратному машинному времени и обеспечивающему большее значение ![]() . Как правило, значения
. Как правило, значения ![]() и
и ![]() определяют точку на кривой износа, которая лежит на входе в участок катастрофического износа инструмента.
определяют точку на кривой износа, которая лежит на входе в участок катастрофического износа инструмента.
В случае если в распоряжении исследователя нет данных, необходимых для построения зависимости ![]() , может быть использован теоретический график зависимости
, может быть использован теоретический график зависимости ![]() , то есть кривая износа (см. рис. 5.1 и 5.2).
, то есть кривая износа (см. рис. 5.1 и 5.2).
Метод оптимизации периода стойкости инструмента с использованием кривой износа обычно называют методом профессора Н.Н. Зорева.
Решение уравнения (5.7) приводит нас к уравнению:
![]() ,
,
которое может быть преобразовано к виду
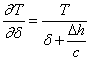 или
или 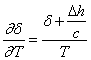 . (5.11)
. (5.11)
Исходя из анализа геометрического смысла производной, мы можем утверждать, что решению уравнения (5.11) будет соответствовать точка на кривой износа, в которой тангенс угла наклона касательной к графику функции ![]() равен
равен 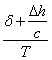 . На рис. 5.5 представлена схема, иллюстрирующая поиск значений
. На рис. 5.5 представлена схема, иллюстрирующая поиск значений ![]() и
и ![]() с использованием кривой износа. Очевидно, для того чтобы с помощью графика зависимости
с использованием кривой износа. Очевидно, для того чтобы с помощью графика зависимости ![]() определить точку
определить точку ![]() , мы должны провести касательную к кривой износа из точки, лежащей ниже начала координат на величину
, мы должны провести касательную к кривой износа из точки, лежащей ниже начала координат на величину ![]() .
.
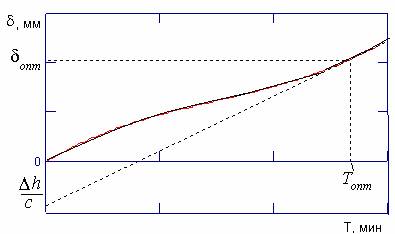
Рис. 5.5 Схема к определению оптимального периода стойкости инструмента по методу Н.Н. Зорева