Из основного уравнения молекулярно-кинетической теории (7.4) газов следует, что средняя квадратичная скорость газовых молекул равна:

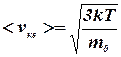.                                                       (7.9)

Если газ находится в состоянии термодинамического равновесия (Т=const), то, как бы не изменялись скорости молекул при столкновениях, скорость  остается постоянной. При этом в газе устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон выведен теоретически Дж. Максвеллом. Максвелл описывает газ, состоящий из очень большого числа () тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре.

Закон Максвелла описывается некоторой функцией  – функцией распределения молекул по скоростям. Если диапазон скоростей разбит на малые интервалы, равные , то каждому интервалу скоростей будет соответствовать некоторое число молекул , имеющих скорость, заключенную в этом интервале.

Функция  определяет относительное число молекул , скорости которых лежат в интервале от  до :

.                                                     (7.10)

Число молекул, обладающих скоростями в интервале , , определяется по формуле:

.

Применяя теорию вероятностей, Максвелл нашел вид функции  – закон распределения молекул идеального газа по скоростям:

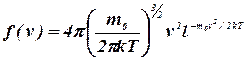,                                  (7.11)

из которой видно, что конкретный вид функции (рис. 7.4) зависит от массы молекул газа (), то есть от рода газа и от параметра состояния – температуры ().

Из формулы (7.10) следует, что:  – относительное число молекул, обладающих скоростями в интервале . Оно равно площади () заштрихованной полоски (рис. 7.4):

.

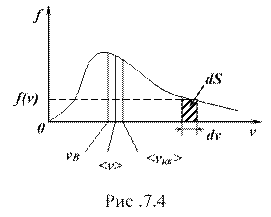
Полный диапазон скоростей заключен между нулем и бесконечностью, поэтому площадь, ограниченная кривой распределения и осью абсцисс, равна:

Это означает, что функция удовлетворяет условно нормировки. Анализ графика показывает, что относительное число молекул, обладающих очень малыми () и очень большими () скоростями, мало. Максимум кривой соответствует наиболее вероятной скорости (). Ее можно найти, продифференцировав выражение (7.11) по аргументу  и приравняв результат к нулю:

.                                         (7.12)

К этой скорости, согласно формулам (7.3) – (7.5), близки по своим значениям <> и  <>.

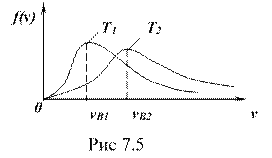Из формулы (7.12) следует, что с увеличением температуры () максимум распределения смещается в сторону больших скоростей. Но площадь, ограниченная кривой, остается неизменной, равной единице, поэтому кривая будет растягиваться и понижаться (см. рис. 7.4.

Среднюю скорость молекул можно определить по формуле:

отсюда

.     (7.13)

Исходя из распределения молекул по скоростям, можно найти распределение молекул газа по значениям кинетической энергии ():

,

где  – число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале энергий :

Функция распределения имеет вид: 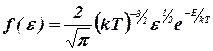, при этом средняя кинетическая энергия поступательного движения молекул идеального газа равна:

.

Эта формула совпадает с полученной ранее формулой (7.8)). Однажды установившееся максвелловское распределение в газе сохраняется. Более того, Больцман показал, что в результате взаимодействия между молекулами, каким бы ни было исходное распределение скоростей молекул, в конце концов, устанавливается максвелловское распределение. Точность максвелловского распределения тем больше, чем больше число молекул () в газе.