Пример 1. Изменить порядок интегрирования в интеграле: 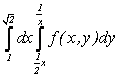 . Область интегрирования изобразить на рисунке.
. Область интегрирования изобразить на рисунке.
 Решение. Выясним вид области интегрирования. Она восстанавливается по рисунку. Так как внутренний интеграл взят по у, то пределы внутреннего интеграла были получены из уравнений
Решение. Выясним вид области интегрирования. Она восстанавливается по рисунку. Так как внутренний интеграл взят по у, то пределы внутреннего интеграла были получены из уравнений ![]() и
и ![]() ; эти линии являются частью границы области интегрирования. Пределы внешнего интеграла постоянны и указывают промежуток изменения переменной х в области:
; эти линии являются частью границы области интегрирования. Пределы внешнего интеграла постоянны и указывают промежуток изменения переменной х в области: ![]() . Для нахождения пределов для внешнего интеграла решим совместно систему:
. Для нахождения пределов для внешнего интеграла решим совместно систему:
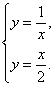
Из системы получим:
![]() и
и ![]() .
.
Вторая точка ![]() не принадлежит области интегрирования. Начертим гиперболу
не принадлежит области интегрирования. Начертим гиперболу ![]() и прямую
и прямую ![]() и учтем, что
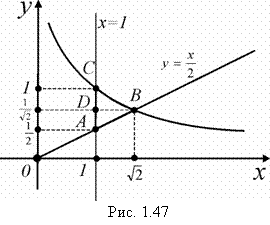
и учтем, что ![]() . Получим область интегрирования АВС (рис. 1.47).
. Получим область интегрирования АВС (рис. 1.47).
Если изменим порядок интегрирования, то внешний интеграл надо брать по переменной у, а внутренний – по х. Из рис. 1.47 видно, что прямые, параллельные оси Ох, все входят в область АВС на СА (х=1), а выходят из неё и на прямой ![]() , и на гиперболе
, и на гиперболе ![]() . Значит, область надо разбить на две. Для этого проводим прямую BD, параллельную оси Ох. Найдем ординаты точек C, D, A. Получим: C(1;1); D(1;
. Значит, область надо разбить на две. Для этого проводим прямую BD, параллельную оси Ох. Найдем ординаты точек C, D, A. Получим: C(1;1); D(1; ![]() ); A(1;
); A(1; ![]() ). Тогда
). Тогда
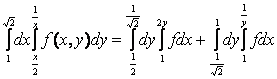 .
.
Пример 2. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной линией ![]() . Сделать схематический чертеж.
. Сделать схематический чертеж.
Решение. Уравнение линии преобразуем к виду:
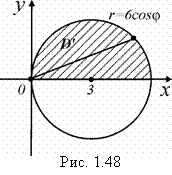
![]()
выделив в левой части заданного уравнения полный квадрат относительно переменной х. Откуда видим, что имеем окружность радиуса 3 с центром в точке С(3;0) (рис. 1.48).
В полярных координатах уравнение этой линии будет:
![]()
или
![]()
Это выражение будет переменным верхним пределом во внутреннем интеграле по r.
Тогда
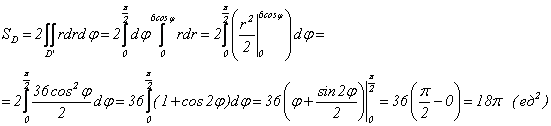
Ответ: ![]() .
.
Пример 3. Дано скалярное поле ![]() и точка М0(1;2;3). Найти направление и величину наибольшей скорости возрастания поля в точке М0.
и точка М0(1;2;3). Найти направление и величину наибольшей скорости возрастания поля в точке М0.
Решение. Известна связь, которая дается формулой (1.94): ![]() Поэтому максимальное значение
Поэтому максимальное значение ![]() будет иметь в направлении
будет иметь в направлении ![]() . Следовательно, найдем сначала
. Следовательно, найдем сначала ![]() :
:
![]()
но
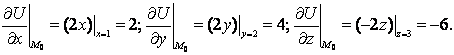
![]()
Направляющие косинусы ![]() дадут нам то уравнение, в котором
дадут нам то уравнение, в котором ![]() будет иметь максимальное значение:
будет иметь максимальное значение:
![]()
![]()
Наибольшая скорость роста поля равна модулю градиента:
![]()
Ответ: ![]()
![]() .
.
Пример 4. Найти векторные линии поля ![]() .
.
Решение. Согласно (1.95) составим систему дифференциальных уравнений векторных линий, зная ![]() :
:
![]() .
.
Отсюда
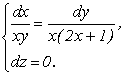
Интегрируя систему, получим:
![]() ,
,
![]()
Таким образом, векторные линии данного поля представляют собой эллипсы с центром в точке (-0.5;0) и полуосями ![]() и
и ![]() :
:
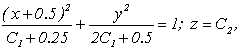
расположенные в плоскостях параллельных плоскости xoy.
Пример 5. Вычислить поток векторного поля ![]() ; через
; через ![]() , вырезанный из плоскости (Р):
, вырезанный из плоскости (Р): ![]() координатными плоскостями, в том направлении нормали к плоскости, которое образует с осью Ох острый угол; а также по формуле Остроградского поток пирамиды, образовавшейся, присоединением к поверхности
координатными плоскостями, в том направлении нормали к плоскости, которое образует с осью Ох острый угол; а также по формуле Остроградского поток пирамиды, образовавшейся, присоединением к поверхности ![]() боковых треугольников, которые лежат в координатных плоскостях (нормаль внешняя).
боковых треугольников, которые лежат в координатных плоскостях (нормаль внешняя).
Решение. Начнем с построения рисунка. Уравнение заданной плоскости лучше записать как уравнение в «отрезках» ![]() (рис. 1.49).
(рис. 1.49).
Определим единичный вектор нормали ![]() , и образующий с осью ох острый угол. Помним, что коэффициенты при x, y, z в уравнении плоскости есть координаты нормального вектора к этой плоскости
, и образующий с осью ох острый угол. Помним, что коэффициенты при x, y, z в уравнении плоскости есть координаты нормального вектора к этой плоскости ![]() Этот вектор имеет положительную проекцию на ось ох, следовательно, образует с этой осью острый угол:
Этот вектор имеет положительную проекцию на ось ох, следовательно, образует с этой осью острый угол:
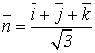 .
.
Согласно формуле (1.101):
![]() .
.
Найдем скалярное произведение ![]() :
:
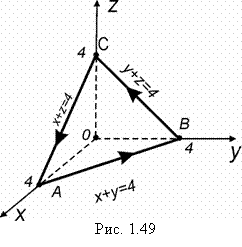
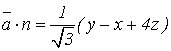 .
.
Отсюда
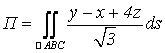 .
.
Чтобы вычислить этот интеграл по поверхности ![]() , заменим его двойным интегралом по проекции D поверхности
, заменим его двойным интегралом по проекции D поверхности ![]() на плоскость хОу. Элемент площади ds:
на плоскость хОу. Элемент площади ds:
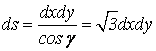
и на поверхности ![]() :
: ![]() .
.
Следовательно,

Вычислим поток этого же векторного поля по формуле Остроградского (1.103), для чего сначала найдем ![]() , используя формулу (1.104):
, используя формулу (1.104):
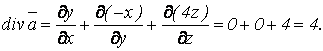
Тогда:

Ответ: ![]()
Пример 6. Вычислить циркуляцию Г поля ![]() вдоль линии АВСА (рис. 1.49) непосредственно и по теореме Стокса.
вдоль линии АВСА (рис. 1.49) непосредственно и по теореме Стокса.
Решение
а) Непосредственное вычисление циркуляции. Контур К=АВ+ВС+СА является кусочно-гладкой линией, состоящей из трех гладких кусков: x + y = 4; y + z = 4; x + z = 4. По свойству аддитивности:
![]() .
.
Вычислим каждое слагаемое правой части:
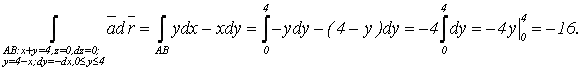
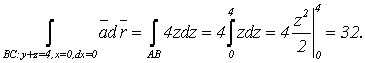
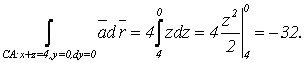
Суммируя полученные результаты, получим: Г = -16.
б) Вычисление циркуляции по теореме Стокса
Согласно (1.110):
![]()
В качестве поверхности S выберем часть плоскости x+y+z=4 (т.е. ![]() ). Найдем единичный вектор
). Найдем единичный вектор ![]() (он найден в примере 5):
(он найден в примере 5): 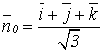 , а также вектор ротор:
, а также вектор ротор:
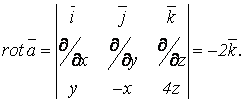
Тогда 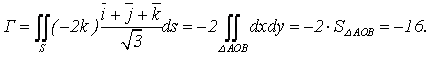
Пример 7. Дано векторное поле ![]() . Требуется узнать: будет ли оно соленоидальным или потенциальным? В случае потенциальности поля найти его потенциальную функцию U(x,y,z).
. Требуется узнать: будет ли оно соленоидальным или потенциальным? В случае потенциальности поля найти его потенциальную функцию U(x,y,z).
Решение. Проверим условие соленоидальности, для чего найдем 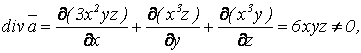 кроме x=0, y=0, z=0. Поле в общем случае не соленоидальное.
кроме x=0, y=0, z=0. Поле в общем случае не соленоидальное.
Найдем вихрь поля:
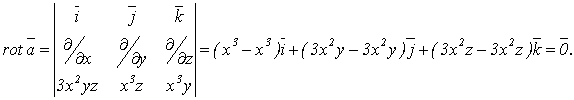
Отсюда: поле потенциально во всем пространстве. Найдем его потенциал по формуле (1.115):

Проверка. Найдем ![]() :
:
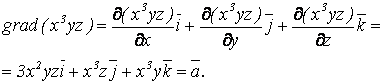
Ответ: ![]() .
.