Построенная нами аналитическая модель операционного анализа ожидая выполнения плановых работ (ПР) 
, поступающих в ПС в оперативном режиме и не имеющих в очередности приема их на выполнение приоритетов, может быть использована и в общем случае, когда в ПС поступает многомерный поток ПР 
, в котором ПР каждого 
-го потока имеют 
-й приоритет в очередности приема их на выполнение.
Метод применения аналитической модели для выполнения в ПС многомерного потока ПР 
с приоритетами строится при следующих качественных предпосылках:
ü многомерный поток ПР состоит из 
одномерных потоков ;
ü для каждого модуля 
проектируемой системы известно допустимое значение коэффициента загрузки 
, связанное только с резервированием его мощности и с ремонтом и профилактикой устройств ;
ü средняя продолжительность ожидания в очереди на выполнение 
у модуля для ПР 
задается в виде доли от средней продолжительности 
выполнения одной плановой работы из -го одномерного потока, равной 
, т.е.
.
Примечание. Значение параметра 
находится по тому же методу, что и значение параметра 
для одномерного потока ПР 
:
,
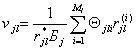где 
— трудоемкость выполнения модулем -й ПР -го 
одномерного потока;
— коэффициент посещения ПР 
из -го одномерного потока модуля , 
;
— мощность 
-го модуля ПС.
Так как
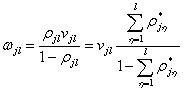, (4.30)
где 
— коэффициент загрузки модуля 
, связанный только с выполнением им ПР из 
-го потока, то из формулы (4.30) следует, что
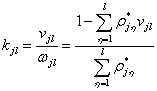, (4.31)
а из формулы (4.31) следует, что
. (4.32)
Приоритет каждой ПР из 
-го потока полностью определяется значением показателя 
: чем меньше , тем выше приоритет ПР из -го потока. Поэтому на основании формулы (4.32) можно утверждать, что, чем выше значение коэффициента 
, тем выше и приоритет у ПР из -го одномерного потока в очередности приема на выполнение модулем .
Целью синтеза ПС для выполнения многомерного потока 
, с приоритетами в очередности их выполнения модулями 
, является решение следующих двух задач.
Задача 4.6. Определить оптимальные значения приоритетов () для ПР , в очередности их выполнения модулями ПС по критерию достижения минимума показателя средней продолжительности 
пребывания ПР 
у модуля при условии, что коэффициент загрузки ограничен сверху, 
.
Решение. Для решения поставленной задачи используется метод Лагранжа при следующей постановке: требуется определить оптимальные значения показателей 
при условии, что
, а 
.
Алгоритм решения состоит в следующем:
1. Строится целевая функция
,
где 
— доля -го одномерного потока в суммарном многомерном потоке, равная
.
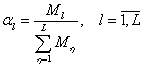2. Находятся частные производные от 
по :
.
3. Решая систему нормальных уравнений
,
где 
, находят уравнение
,
которое имеет два корня
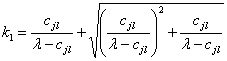; (4.33)
.
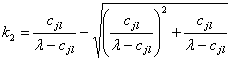Так как корень 
, действительным корнем является только 
.
Для определения значения показателя 
по формуле (4.34) необходимо предварительно найти значение неизвестного параметра 
, для чего используется равенство (4.32) и условие
. (4.34)
Из равенств (4.32), (4.33) и (4.34) следует, что
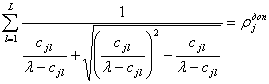. (4.35)
Значение параметра находится из равенства (4.35) методом последовательных приближений:
,
где 
— шаг итерации.
После определения значений для всех 
модулей ПС и всех одномерных потоков 
находят значения следующих показателей:
— коэффициента загрузки модуля ПР 
;
— средней продолжительности пребывания каждой ПР в очереди у модуля 
;
— средней продолжительности пребывания каждой ПР у модуля
;
— средней продолжительности пребывания одной ПР в ПС
.
Задача 4.7. Минимизировать значения системных потенциалов 
, модулей ПС при ограничении 
средней продолжительности нахождения каждой работы 
в ПС. Отметим, что при решении этой задачи значения параметров 
задаются только экспертами по одномерным потокам ПР 
исходя из значимости ПР каждого одномерного потока.
Решение. Для решения данной задачи, так же, как и задачи 4.6, применяется метод Лагранжа. Для его использования вводится понятие системного потенциала для каждого модуля ПС. Считается, что системный потенциал модуля 
есть
. (4.36)
При возрастании мощности 
модуля и коэффициента значение системного потенциала 
возрастает: в первом случае – из-за увеличения скорости выполнения модулем ПР , во втором случае – из-за уменьшения времени пребывания ПР у модуля в очереди на выполнение. С увеличением трудоемкости 
выполнения ПР модулем значение уменьшается, что также очевидно.
Поэтому целью решения данной задачи является уменьшение системного потенциала каждого модуля ПС при условии, что среднее время пребывания каждой ПР в ПС не будет превышать заданной величины 
.
Для решения поставленной задачи синтеза ПС строится целевая функция
(4.37)
На основании того, что
,
,
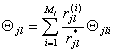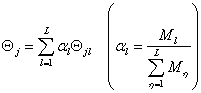и формулы (4.36) целевая функция (4.37) приводится к виду
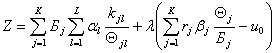, (4.38)
где
.
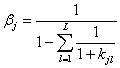Приравняв частные производные от целевой функции (4.38) нулю, получаем систему нормальных уравнений
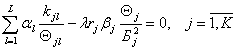. (4.39)
Решая систему уравнений (4.39) относительно 
, находим
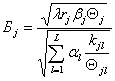(4.40)
где
.
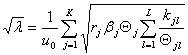Мощность модуля 
, определяемая по формуле (4.40), является оптимальной по критерию
и 
.
Остальные показатели рассмотренной ПС определяются по формулам, приведенным в многокритериальном методе синтеза проектируемых систем.
Решение типовых задач по анализу управления в ПС
Все типовые задачи, решаемые с применением статистической модели операционного анализа, полностью решаются и с помощью аналитической модели операционного анализа. Для их решения так же, как и для статистической модели, достаточно, чтобы предварительно были определены по каждой задаче все описанные ранее исходные параметры. Рассмотрим выполнение указанных операций отдельно по каждой задаче.
Задача 4.8. Исходные данные по статистической модели: 
, 
, 
, 
. В аналитической модели эти данные определяются следующим образом. Интенсивность находится одним из трех способов:
1) если известно количество выполняемых работ 
за время 
, то 
;
2) если известна величина 
, то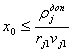 
;
3) если известны данные по материальным ресурсам, приведенные в табл. 4.1, то 
, где 
и 
есть производительность ПС, полученная соответственно без учета интенсивности поступления материальных ресурсов и только на основании интенсивности поступления материальных ресурсов.
— мощность 
-го модуля ПС находится либо по формуле (4.22), если не указано ограничение (4.25), либо по формуле (4.29), если это ограничение указано;
— частота перехода выполняемой работы в ПС от модуля 
к модулю находится по формуле (4.20).
Задача 4.9. Если в статистической модели при решении данной задачи выполняется уравнивание (балансировка) коэффициентов загрузки всех модулей исследуемой системы, то в аналитической модели проектируемая система создается уже сбалансированной. При этом балансирование загрузки модулей в ней выполняется с учетом двух критериев:
и 
.
Задача 4.10 – 4.12. Данные задачи решаются с помощью аналитической модели операционного анализа таким же образом, т.е. по идентичным алгоритмам, как и в случае применения статистической модели. Однако в аналитической модели исходные данные, используемые для их решения по параметрам 
и 
, могут быть заданы с учетом ограничений и . Для этого достаточно, чтобы исходные параметры , определялись по формуле
,
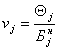где 
, находятся по формуле (4.21), а 
— по формуле (4.29).
Дополнительно к указанному выше отметим, что при использовании аналитической модели можно также определить по формуле (4.30) и минимальную стоимость проектируемой системы в целом.
Задача 4.13. Для проектируемой системы известны следующие исходные данные: 
. Требуется следующее:
ü найти точку 
, в которой скорости изменения значений 
и 
совпадают;
ü определить, во сколько раз изменится значение суммарной стоимости производственных ресурсов ПС при уменьшении величины 
в 5 раз.
Решение. Из формулы (4.30) следует, что функция 
является гиперболической и может быть записана в виде 
, где 
есть постоянная величина, равная
.
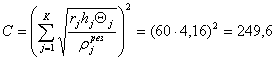Значения параметров 
и 
находятся из условия
,
откуда следует, что
. (4.41)
При уменьшении и увеличении значения параметра в 5 раз получается 
и 
.
Из анализа результатов решения данной задачи следует, что изменение значения критериального параметра 
существенно влияет на суммарную стоимость производственных ресурсов проектируемой системы в целом. Поэтому задание критерия 
является весьма ответственной задачей. На практике в большинстве случаев целесообразно принимать 
, где находится по формуле (4.41).
Задача 4.14. Оценка нормативных значений продолжительности выполнения работ в подсистемах производственной системы. Актуальность решения данной задачи следует прежде всего из того, что от точности определения средних значений продол
жительности 
выполнения каждой работы в каждой 
-й 
подсистеме исследуемой производственной системы во многом зависит адекватность аналитической модели моделируемой реальной системе. Кроме того, излагаемый алгоритм оценки значений может эффективно использоваться в реальных производственных системах для определения соответствия нормативных значений , задаваемых в виде сборников расценок на выполняемые работы, специфике каждой рассматриваемой системы.
Постановка задачи: задано нормативное значение средней продолжительности выполнения одной работы в -й подсистеме исследуемой производственной системы, определяемой по формуле
.
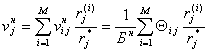Так как 
есть средняя величина, полученная по случайной выборке 
, то она тоже является случайной величиной со средним квадратичным отклонением
.
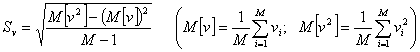Используя статистическую модель операционного анализа, находим для каждой подсистемы исследуемой системы значения 
, где 
— средняя продолжительность времени из интервала наблюдения 
, в течение которого подсистема
была занята работой, а 
— число работ, выполняемых в в интервале наблюдения . Так как определяется по результатам наблюдений, то ее будем считать фактической величиной и обозначать 
.
Для полной оценки величины необходимо найти точечную и интервальную оценки.
Точечная оценка тождественна точечной оценке нормативной мощности 
модуля 
исследуемой системы. Она определяется либо в виде относительной величины отклонения 
от ее нормативного значения, т.е. от 
, либо в процентах:
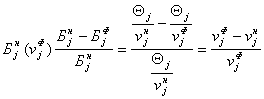
или
.
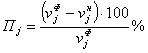Интервальная оценка величины 
состоит в определении максимального значения вероятности того, что величина 
принадлежит доверительному интервалу 
, где 
есть параметр нормального распределения вероятностей:
.
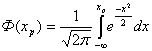Значения определяются по таблице функции 
по заданной доверительной вероятности 
. Для оперативного определения значений при 
можно воспользоваться табл. 4.2.
Таблица 4.2
Таким образом, если выполняется условие 
, то справедливо считать, что с заданной доверительной вероятностью величины 
и 
совпадают.
Изложенный метод точечной и интервальной оценок показателей 
, исследуемой системы, по сути, является методом оценки физического и морального устаревания производственных ресурсов ее модулей.