Пусть на плоскости хОу задана дуга М0М, которая имеет длину, и на ней задана функция Х(х, у) (рис. 1.1).
Выполним операции:
1) разобьём произвольно дугу М0М на n частей точками М0, М1,… Мn = М;
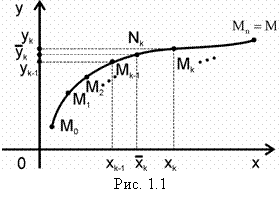 2) в каждой дуге Мk-1Мk выберем произвольно по точке
2) в каждой дуге Мk-1Мk выберем произвольно по точке ![]() и вычислим Х(Nk);
и вычислим Х(Nk);
|
3) умножим ![]() на приращение
на приращение ![]() ;
;
4) составим интегральную сумму:
![]() ; (1.9)
; (1.9)
5) найдем предел суммы (1.9) при стремлении к нулю наибольшей из длин частных дуг (максимального диаметра разбиения ![]() ). Этот предел (в случае непрерывной функции Х(х, у) можно доказать, что существует) называется криволинейным интегралом от Х(х, у) по переменному х вдоль кривой М0М и обозначается через
). Этот предел (в случае непрерывной функции Х(х, у) можно доказать, что существует) называется криволинейным интегралом от Х(х, у) по переменному х вдоль кривой М0М и обозначается через
![]() (1.10)
(1.10)
Аналогично определяется криволинейный интеграл от Y(x,y) по переменному у:
![]() (1.11)
(1.11)
Если кривая М0М задана в пространстве XYZ и на кривой заданы непрерывные функции Х(х, у, z), Y(х, у, z)и Z(х, у, z), то поступая подобно плоскому случаю, определяют криволинейные интегралы вдоль кривой М0М:
![]() (1.12)
(1.12)
![]() (1.13)
(1.13)
![]() (1.14)
(1.14)
Вводят составной криволинейный интеграл как для плоского случая, так и пространственного и обозначают:
![]() (1.15)
(1.15)
и
![]() . (1.16)
. (1.16)
Отметим, что из определения вытекают следующие свойства криволинейных интегралов второго рода (мы рассмотрим свойства на ![]() , но они имеют место и для интегралов (1.11) – (1.16)).
, но они имеют место и для интегралов (1.11) – (1.16)).
1) При перемене направления дуги (пути интегрирования) криволинейный интеграл изменит только свой знак:
![]() .
.
2) Постоянный множитель можно вынести за знак интеграла:
![]() .
.
3) Криволинейный интеграл от суммы конечного числа слагаемых равен сумме криволинейных интегралов слагаемых.
4) Если путь интегрирования М0М разбить на части, например М0А и АМ (свойство аддитивности), то (рис. 1.2,а)
![]() . (1.17)
. (1.17)
5) Криволинейный интеграл вдоль замкнутой кривой, взятый при заданном направлении обхода, не зависит от выбора начальной точки (рис. 1.2,б.).
а) б)
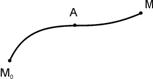
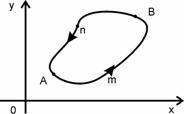
Рис. 1.2
Доказательство:
![]()
Правые части последних равенств равны, поэтому равны и левые части.
Перейдем к вопросу вычисления криволинейных интегралов по координатам.
Пусть направленная кривая К пространства задана параметрическими уравнениями: x = x(t), y = y(t), z = z(t), ![]() , где функции x(t), y(t) и z(t) – имеют непрерывные производные по t и x = х(М0), xm = x(М). Тогда при нашем разбиении (см. определение (1.9),
, где функции x(t), y(t) и z(t) – имеют непрерывные производные по t и x = х(М0), xm = x(М). Тогда при нашем разбиении (см. определение (1.9),
точки Мк(xk,yk), соответствующие этим t, разобьют дугу М0М также на n частей. По формуле Лагранжа получим:
![]()
где ![]() и
и ![]() .
.
Суммируя, найдем:
![]() (1.18)
(1.18)
где левая часть (I.3.10) есть интегральная сумма для криволинейного интеграла от Х(х,у), а правая часть является интегральной суммой для определенного интеграла по переменной t. Перейдя к пределу при ![]() , получим:
, получим:
![]() (1.19)
(1.19)
Аналогично можно получить формулы и для всех других криволинейных интегралов. Запишем правило интегрирования для пространственного случая (для плоского случая рекомендуется сформулировать самостоятельно, подобно приведенному).
Правило: для вычисления криволинейного интеграла (1.16) следует в подынтегральном выражении заменить x, y, z, dx, dy, dz их выражениями из уравнений пути интегрирования и вычислить определенный интеграл от полученного выражения в пределах наименьшего и наибольшего изменения параметра:
![]() (1.20)
(1.20)
![]() .
.
Методическое руководство
1) На практике часто бывает необходимо составлять уравнения пути интегрирования, если имеют дело с прямолинейными участками его, тогда используют уравнения прямой, проходящей через две заданные точки:
![]() (1.21)
(1.21)
приравняв эти отношения параметру t , получают связь x(t), y(t) и z(t), и соответствующие граничные его значения для расстановки пределов интегрирования.
2) Если кривая интегрирования плоская, то за параметр выбирают одну из координат.
Отметим, что в случае криволинейного интеграла второго рода механический смысл его следует из соотношения (1.20) и выражает работу в случае задания силового поля ![]() , т.е., когда X,Y,Z – проекции этой силы на оси координат.
, т.е., когда X,Y,Z – проекции этой силы на оси координат.
Пример 1
Вычислить ![]() , где АВ – прямая, соединяющая О(0, 0) с А(1, 2).
, где АВ – прямая, соединяющая О(0, 0) с А(1, 2).
Решение. Согласно правилу и методическому руководству уравнение прямой ОА: y = 2x ![]() . Отсюда dy = 2dx и
. Отсюда dy = 2dx и
![]() .
.
Пример 2
Условие примера 1, а путь ОА – парабола с вершиной О и осью Оу ![]() .
.
Решение. Уравнение параболы имеет вид ![]() . Так как парабола проходит через точку А(1; 2), то
. Так как парабола проходит через точку А(1; 2), то ![]() и k = 2, а y = 2x2, откуда dy = 4xdx,
и k = 2, а y = 2x2, откуда dy = 4xdx, ![]() :
:
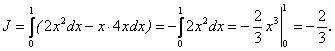
Пример 3
Условие примера 1, а путь ОВА – ломаная, где В(1;0) (сделайте рисунок).
Решение. Используя свойство аддитивности (1.17) получим:
![]()
Так как уравнение ОВ: y = 0 ![]() , то dy =0; а уравнение ВА: х = 1
, то dy =0; а уравнение ВА: х = 1 ![]() ; поэтому dx = 0:
; поэтому dx = 0:
![]()
Пример 4
Вычислить ![]() вдоль отрезка прямой АВ от А(1;1;3) до В(3;2;1).
вдоль отрезка прямой АВ от А(1;1;3) до В(3;2;1).
Решение. Используя (1.21), составим параметрические уравнения прямой:
![]()
Значение tA = 0 и tB = 1; x’(t) = 2; y’(t) = 1; z’(t) = -2. По формуле (1.20):
![]()
Пример 5
Вычислить ![]() вдоль дуги y = x2 от А(0;0) до В(2;8).
вдоль дуги y = x2 от А(0;0) до В(2;8).
Решение. Примем х за параметр, по формуле (1.20):
![]()
будем иметь:
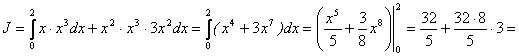
![]()
Задачи для упражнений
1) Найти ![]() , если АВ: =3х2, А(0;0), В(1;3).
, если АВ: =3х2, А(0;0), В(1;3).
Ответ:16.
2) Найти ![]() , если АВ: x = t, у = t2, z = 3 – t, причем tA = 1, tB = 2.
, если АВ: x = t, у = t2, z = 3 – t, причем tA = 1, tB = 2.
Ответ: ![]() .
.
3) Найти ![]() , вдоль АВ: у = х2, А(1;1) до В(2;4).
, вдоль АВ: у = х2, А(1;1) до В(2;4).
Ответ: 31.
4) Вычислить  , где К – отрезок прямой х + у = 1
, где К – отрезок прямой х + у = 1 ![]() .
.
Ответ: ![]() .
.
1) Вычислить 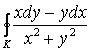 , где К : x = а cos t, y = a sin t
, где К : x = а cos t, y = a sin t ![]() .
.
Ответ: ![]() .
.