Положение точки в пространстве задают координатами, отличными от декартовых. Наиболее употребительной системой является цилиндрическая система (рис. 1.23), где r и  – полярные координаты точки Р (проекции М на плоскость xОy и аппликатой z).

Координаты называются цилиндрическими.  Связь этих координат с декартовыми дается формулами:

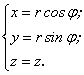                             (1.65)

Фактически мы уже использовали цилиндрические координаты, решая пример в разд. 1.2.4 (точка лежит на поверхности цилиндра).

Другой вид координат – сферические координаты (рис. 1.24). Положение точки M задается её расстоянием R от начала координат, полярным углом  проекции Р на xОy и углом  между осью ОZ и радиус-вектором ОМ (точка лежит на поверхности сферы):

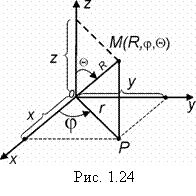
Связь между декартовыми (x, y, z) и сферическими координатами  точки М:

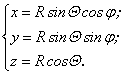                               (1.66)

Тройной интеграл в цилиндрических координатах имеет вид:

      (1.67)

Тройной интеграл в сферических координатах:

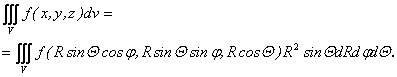                  (1.68)

Можно выбрать конкретный порядок интегрирования, например:

                                 (1.69)

При выборе других порядков интегрирования можно записать и другие формулы.

Для сферической системы координат расстановку пределов в общем случае не будем рассматривать, а запишем, например, для тела V – сферы с центром в начале координат:

Пример 1

Найти объем тела, ограниченного поверхностями  (рис. 1.25).

Решение. Тело симметрично относительно  ОХ и ОY. Найдем четвертую часть объема, расположенную в первом октанте, тогда получим и весь объем.

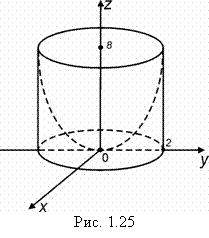Используем цилиндрические координаты. Уравнения поверхности , плоскости  и окружности  в цилиндрических координатах :

.

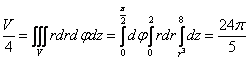Отсюда: .

Пример 2. Найти массу лежащей в первом октанте части V шара радиуса а, если плотность  в точке (x, y, z) равна:  = .

Решение. Согласно (1.46)

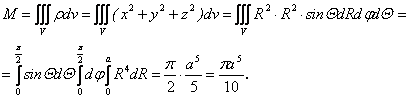
Задачи для упражнений

1) Найти объём цилиндра: ,                 Ответ:

2) Найти объём сферы: .                                      Ответ: .