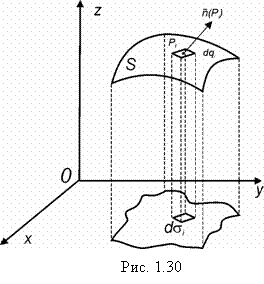
Рассмотрим поверхность S, которая задана функций 
, предполагаем, что любая прямая, параллельная оси Оz, пересекает её не более чем в одной точке (рис. 1.30). Считаем, что выбрана верхняя сторона.
Предположим, что функция 
есть непрерывная на S. Разобьем её на n частей: 
.
На части 
(I = 1,…,n) возьмем точку 
и соответствующее значение умножим на площадь проекции на xОy: 
. Составим сумму 
– она называется интегральной.
Определение: 
называется поверхностным интегралом второго рода от функции Z(x, y, z) по выбранной стороне по координатам x и y и обозначается:
Итак,
(1.80)
Аналогичным образом определяются поверхностные интегралы:
и 
,
то есть
; (1.81)
. (1.82)
Вводят обобщенный (комбинированный) поверхностный интеграл по координатам:
(1.83)
Исходя из определения, отметим важное свойство, присущее этим интегралам: при перемене стороны поверхности интеграл изменяет только свой знак.
Методическое руководство: при вычислении поверхностных интегралов второго рода следует руководствоваться правилом, которое следует из определения: если S является куском цилиндрической поверхности, образующая которой параллельна одной из координатных осей, то соответствующий поверхностный интеграл равен нулю. Например:
· если оси Оz, то 
;
· если оси Ох, то 
;
· если оси Оy, то 
,
так как при этом соответствующая площадь проекции 
.
Сформулируем правило вычисления поверхностного интеграла второго рода для одного из них (доказательство аналогично вычислению криволинейного интеграла второго рода).
Вычисление поверхностных интегралов второго рода неизменно сводится к вычислению обычных двойных интегралов. Пусть, например, поверхность S задана уравнением 
с выбранной ориентацией в сторону роста z, тогда
. (1.84)
Пример
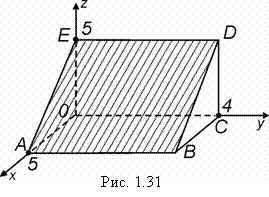
Вычислить 
, где S – верхняя сторона части плоскости x + z = 5, отсеченной плоскостями y = 0, y = 4 и лежащей в 1 октанте (рис. 1.31).
Решение. Согласно (1.83):
.
Согласно методическому руководству, наша поверхность (плоскость) имеет ось Оy, параллельную образующей, поэтому 
.
Вычислим:
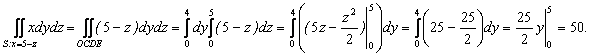
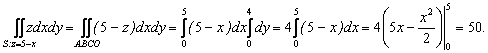
Итак, J = 50 + 50 = 100.