Сложение, вычитание или умножение двоичных чисел выполняются так же, как и в арифметике десятичных чи­сел. На рис. 1.4 представлены простые правила двоичного сложения. Два первых (рис. 1.4, а и 1.4, б) правила очевидны, третье (рис. 1.4, в) показывает, что 1 + 1 = 10, то есть происходит перенос в следующий (старший) разряд. Результатом явля­ется сумма – 0 с переносом 1. Четвертое правило (рис. 1.4, г), показывает, что, если первое и второе слагаемые равны 1 и есть перенос из предыдущего (младшего) разряда, то в этом случае имеем: 1 + 1 + 1 = 11, то есть результатом явля­ется сумма – 1 с переносом 1

.

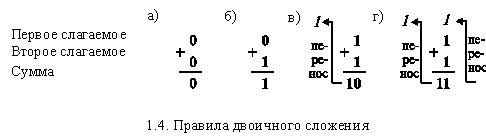Покажем операцию сложения двоичных чисел на примере:

Цифры разрядов суммы формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы образуется суммированием цифр младших разрядов слагаемых. При этом, кроме цифры разряда суммы формируется цифра переноса в следую­щий, более старший разряд. Таким образом, в разрядах, начиная со второго, суммируются три цифры: цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего.

Перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде равен или больше р = 2 (основание системы счисления).

На рис. 1.6 приведены правила двоичного вычитания. Первые три (рис. 1.6, а, 1.6, б, 1.6, в) аналогичны десятичному вычитанию. Послед­нее правило (рис. 1.6, г) требует заёма из более значимого предшествующего разряда. Уменьшаемым является дво­ичное число 10, вычитаемым 1, разностью – 1.

Вычтем двоичное число 00111001 из 01. Этот пример приведен на рис. 1.7. Младшие (крайние справа) три разряда это­го двоичного вычитания просты для выполнения и относят­ся к первым трем правилам на рис. 1.6. В колонке 4-го разряда имеет место вычитание 1 из 0. Тогда 1 занимается из колонки 5-го разряда. Единица вычитается из 10₂, что дает раз­ность 1 согласно четвертому правилу на рис. 1.6. После этого заема в колонке 5-го разряда имеет место вычитание 1 из нового вычитаемого 0. Согласно четвертому правилу, 1 дол­жна быть занята из следующей, более значимой позиции (колонка 6-го разряда), но в колонке этого разряда имеем 0, поэтому мы должны сделать заем из колонки 7-го разряда, что и вы­полнено. Окончательно колонка 5 делает заем из колонки 6, уменьшаемым в колонке 5 становится 10₂, вычитаемым 1, разностью 1. В колонке 6 имеем 1 – 1 = 0, в колонке 7: 0 – 0 = 0, в колонке 8: 0 – 0 = 0. Таким образом, рис. 1.7 иллюстрирует операцию вычитания 00111001₂ из 01₂.

Приведем правила десятичного умножения:

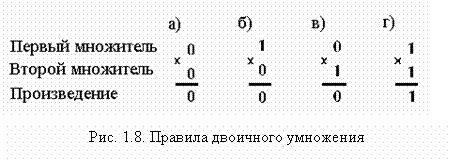
Три первых правила (рис. 1.8, а, 1.8, б и 1.8, в) не требуют никаких пояснений, когда один из множителей равен нулю, произведение равно 0. Четвертое правило (рис. 1.8, г) показывает, что произведение двух единиц равно 1.

Выполним умножение 1101 на 101. Как и в случае умно­жения десятичных чисел, множимое сначала умножается на число, стоящее в младшем разряде (в рассматриваемом случае – бит в колонке веса 1).

Поскольку бит множителя в разряде веса 1 является 1, множимое копируется и составляет первое частичное про­изведение. Вторым битом множителя является 0, тогда вто­рое частичное произведение есть 0000 (заметим, что оно сдвинуто на одну позицию влево). Битом 3-го разряда второго множителя является 1, тогда для получения третьего час­тичного произведения снова следует копирование множи­мого (заметим, что копирование завершается новым сдвигом на одну позицию влево). После этого выполняем сложение трех частичных произведений, что дает результат 1000001₂.