Определение. Векторной линией поля  называется векторная функция  точки М вместе с областью её определения [5].

Задание векторного поля  равносильно заданию трёх скалярных функций , , , являющихся проекциями  на координатные оси:

.

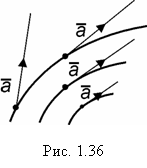
Определение. Векторной линией поля  называется такая линия L, в каждой точке которой касательная совпадает с направлением вектора  (рис. 1.36).

Векторная линия обычно называется линией тока при ламинарном течении жидкости (газа) и др. для поля скоростей, силовой линией – для силового поля и др.

Совокупность всех векторных линий, проходящих через точки куска поверхности вращения S, называются векторной трубкой.

Из определения векторной линии следует, что вектор  параллельный . Из условия коллинеарности векторов  и  следует:

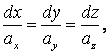                                     (1.95)

где       a_x, a_y, a_z – заданные функции от x, y, z; и (1.95) является системой дифференциальных уравнений векторных линий.

Таким образом, задача нахождения векторных линий поля  равносильна задаче нахождения интегральных кривых системы (1.95).

Пример 1

Найти векторные линии поля .

Решение. Составим систему (1.95):

Интегрируем систему. Получим:

семейство параболических цилиндров

;

семейство параболических цилиндров

.

Семейством векторных линий являются линии пересечения названных цилиндров.

Пример 2

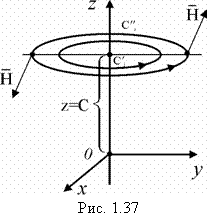
Найти векторные линии магнитного поля (вектор напряженности магнитного поля), образованного постоянным электрическим током I, текущим по бесконечно длинному проводу, совпадающему с осью Оz (рис. 1.37).

Решение. Как известно вектор напряженности магнитного поля равен:

.

Проекции  на оси:

Дифференциальное уравнение векторных линий имеет вид:

.

Последнее отношение имеет смысл когда z = c – постоянная величина. Оставшееся уравнение запишем так:  Интегрируя, получим:

.

Следовательно, векторные линии поля  определяются уравнениями: , z = c. Они являются окружностями с центрами на оси Оz, лежащие в плоскостях, перпендикулярных к этой оси (т.е. линии пересечения цилиндров и плоскостей) (рис. 1.37).

Пример 3

Вектор  линейных скоростей частиц жидкости, вращающейся вокруг оси Оz с постоянной угловой скоростью , может быть представлен в виде , где  – вектор угловой скорости, направленной по оси Оz;  . точки M(x, y, z).

Найти векторные линии поля.

Решение. Найдем сначала вектор .Он будет найден как векторное произведение векторов  и :

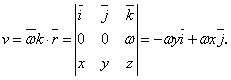
Видно, что задачу свели к предыдущей (вектор ).

Рекомендуется в качестве упражнения проделать шаги до конца.