Задача 1

Число x = 12.371 содержит 3 верные значащие цифры, определить, какова относительная погрешность этого числа.

Решение

По определению верной значащей цифры

12.371,              Dx = 0.05,       .

Отметим, что в данной задаче абсолютная погрешность Dx для любого x представляется в виде 5×10ⁿ, где значение n зависит от числа верных значащих цифр.

Ответ:  dx = 0.004  (либо dx = 0.4%).

Задача 2

Определить сколько верных значащих цифр содержит число x = 1.415, если относительная погрешность этого числа составляет 1%.

Решение

Сначала, зная x и его относительную погрешность, найдём абсолютную погрешность, а затем по определению верных значащих цифр найдём их количество:

x     = 1.415, , следовательно  , Δx = 0.01.

x     = 1.415.

Dx  = 0.01, следовательно число x содержит две верные значащие цифры.

Ответ: число x содержит две верные значащие цифры (1, 4).

Задача 3

Даны числа a и b с абсолютными погрешностями  Da и Db. Найти относительные погрешности суммы, разности, частного и произведения этих чисел.

Дано:

a = 2.35;  Da = 0.01;

b = 3.41; Db = 0.02;

S = a + b; M = a – b; P = ab; Q = a/b.

Найти: d_S, d_M, d_P, d_Q.

Решение

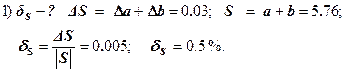
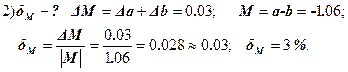
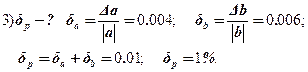
Ответ:

Задача 4

Найти абсолютную и относительную погрешность вычисления значения функции f:

,          

Решение

Сначала найдем относительную погрешность вычисления значения f, а затем абсолютную погрешность. Функция f положительна и дифференцируема, поэтому воспользуемся формулой:

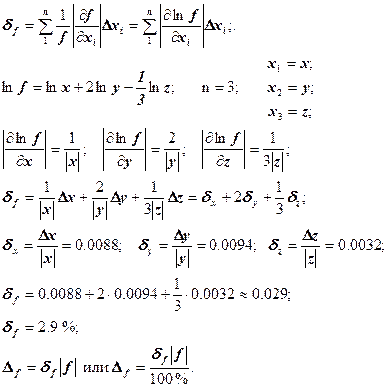
Так как , то значение функции f содержит 2 верных знака. Вычисляем  и записываем   (число содержит две верные значащие цифры и одну сомнительную).

.

Ответ: .