Упорядоченную совокупность n действительных чисел х_1, х_2,…,х_n  называют точкой с этими координатами: М (х_1, х_2,…,х_n). Множество всевозможных точек называется арифметическим n-мерным пространством и обозначается символом Аⁿ. Арифметическое n-мерное пространство называется n-мерным евклидовым пространством, если для любых двух точек  определено расстояние , и обозначается символом Еⁿ.

Функция, заданная на некотором множестве D арифметического n-мерного пространства, называется функцией  n аргументов (независимых переменных):  или , где .

Для случая n = 2, то есть когда множество D – множество точек плоскости (х₁, х₂) º (x, y), то функция у = f(М) — функция двух независимых переменных, что обычно записывают z = f(x, y). Если n = 3, то получаем функцию трёх переменных u = f(x, y, z). Область D – область определения функции двух переменных представляет некоторое множество точек плоскости.

Графиком функции z = f(x, y) называется множество точек Z(x, y,  f(x, y)) трёхмерного пространства и представляет некоторую поверхность, состоящую из этих точек.

Например, множество точек z = x² + y² - параболоид вращения, а множество точек x² + y² - z² = 0 – конус второго порядка.

Отметим, что запись функции z = f(x, y) называется явным её заданием, а F(x, y, z) = 0 – неявным.

1)  Предел функции z = f(x, y), когда :

.

2) Непрерывность функции z = f(x, y):

.

или                                                   .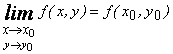

3)  Частные производные функции z = f(x, y) по переменным х и у:

.

4)  Полный дифференциал функции z = f(x, y):

dz = ,

где                                                             .

Если , то

.

5)  Применение дифференциала в приближенных вычислениях функции:

,            .

6)  Производная функции  по направлению вектора :

           ,

где                            ; .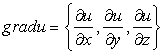

7)  Необходимое условие экстремума дифференцируемой функции u = f(x,y,z):

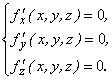
8)  Достаточное условие экстремума:

если ,  и    , тогда:

а) если , то функция имеет экстремум: максимум при A < 0 (или С < 0), минимум при A > 0 (C > 0);

б) если , то экстремума нет.

9)  Если P(x,y)dx+Q(x,y)dy является полным дифференциалом в области D, то

.

10) Уравнение касательной плоскости к поверхности  в точке M₀ (x₀, y₀, z₀):

.

11)  Уравнение нормали к поверхности F(x,y,z) = 0:

.

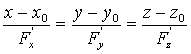Частные производные вычисляются в точке M₀ (x₀, y₀, z₀).

Пример 62:  Найти значения частных производных функции  в точке .

Решение:  используя определение частных производных, видим, что они находятся по известным правилам как в случае функции одной переменной, только следует считать те переменные, по которым не берут производных считать как постоянные, так:

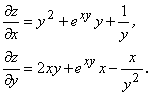
Значения производных в точке  будут:

.

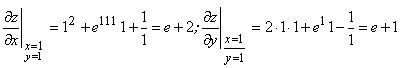Пример 63:  Вычислить приближенно .

Решение:  так как требуемое значение является значением функции , то в качестве , тогда

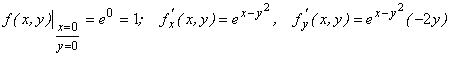
и                                                

                                                   .

Пример 64: Вычислить полный дифференциал функции z = xy при переходе от точки M₀(5;4) к точке M₁(4,8; 3,9).

Решение:  Найдем z¢_x = y,  z¢_y = x,  тогда dz = ydx + xdy. Подставляя в эту формулу

.

Пример 65: Записать уравнение касательной плоскости и нормали к поверхности z = 2 — (x² + y²) в точке M₀(1;1;0).

Решение:  так как F(x,y,z) = z + x² + y² - 2, то  F¢_x = 2x,  F¢_y = 2y,  F¢_z = 1 и при x = 1, y = 1, z = 0 имеем: F¢_x (M₀) = 2,  F¢_y (M₀) = 2,  F¢_z (M₀) = 1. Согласно уравнениям касательной плоскости и нормали к поверхности, будем иметь: 2(x — 1) + 2(y — 1) + (z — 0) = 0, 2x + 2y + z – 4 = 0  —  уравнение касательной плоскости;  — уравнение нормали.