Мы напомним здесь основные операции и известные ранее результаты.

Сложение комплексных чисел z₁ = x₁ + iy₁  и  z₂ = x₂ + iy₂ определяется равенством z₁ + z₂ = (x₁+x₂) + i(y₁ + y₂), а вычитание – действие, обратное сложению.

Произведение  z₁·z₂ = x₁·x₂ – y₁y₂ + i(x₁y₂ + x₂y₁)

Из определения произведения следует, что i·i = i² = -1, а также, что z·z = x²+y², где z = x+iy, а число z = x – iy называется сопряженным к числу   z = x + iy. Деление определяется как действие, обратное умножению.

Умножение и деление чисел в тригонометрической форме записи получили исходя из правил умножения и деления этих числе в алгебраической форме. Для чего представляем числа в тригонометрической форме:

z₁ = r₁ (cos j₁ + i sin j₁); z₂ = r₂ (cos j₂ + i sin j₂).

Тогда

z₁·z₂=r₁·r₂[(cos j₁cos j₂–sin j₁sin j₂) + i (cos j₁sin j₂ + cos j₂sin j₁)]

откуда

z₁·z₂ = r₁r₂ [cos (j₁+ j₂) + i sin (j₁+ j₂)].                                    (2.10)

Деление чисел приводит к формуле:

[cos (j₁– j₂) + i sin (j₁– j₂)],  z₁ ¹ 0,  z₂ ¹ 0.                              (2.11)

Выводы:

1) При умножении чисел в тригонометрической форме модули перемножаются, а аргументы их складываются;

2) При делении – модули делят, а аргументы вычитают:

; Arg()=Argz₁–Argz₂.

Из правила умножения следует, что

zⁿ = rⁿ [cos(nArgz) + i sin(nArgz)],   n є N.                                  (2.12)

При |z| = 1 имеем : zⁿ = cos nj + i sin nj = (cos j + i sin j)ⁿ – эта формула называется формулой Муавра.

Извлечение корня. Пусть n є N. Для данного комплексного числа z решим уравнение z = wⁿ и назовем его корнем степени n из числа z. Когда z = 0, то все значения = 0. Пусть z ¹ 0. Представим z и w в тригонометрической форме:

z = r(cos j + i sin j), w = p(cosq + i sinq).

Так как z = wⁿ, то

или

pⁿ(cos nq + i sin nq) = r(cosj + i sinj).

Из равенства комплексных чисел следует:

pⁿ = r; nq = j + 2kp, (k = 0, ± 1, …).

Отсюда:  p =  – арифметическое значение; 

q = .

Итак,

.                     (2.13)

Пример 1

Найти .

Решение. Представим число z = -i в тригонометрической форме:

r = 1, tg j ® -¥ Þ j = ;.

-i = 1[cos() + i sin()].

Применим (2.13) при n = 3, получим:

 = (cos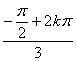+ i sin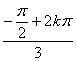), k=0, 1, 2.

При:                               k=0, ()₀=cos– i sin;

k=1, ()₁=cos+ i sin= 0 + i = I;

k=2, ()₂= cos + i sin

Из математического анализа известны разложения e^x, cos x и sin x в степенные ряды. Эти разложения имеют место и для рядов с комплексными членами. Поэтому для комплексного переменного:

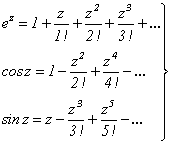                                                 (2.14)

Полагая вместо z величину ij в первую из формул (2.14) и, учитывая, что i² = –1, i³ = –i, …, получим:

e^ij = 1++…=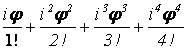

=(1–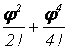–…) + i (j–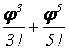–…) = cos j + i sin j.

Итак,

e^ij = cos j + i sin j .                                                     (2.15)

Формула (2.15) называется формулой Эйлера. Заменяя здесь j  на  –j, получим:

e^–ij = cos j – i sin j .                                                     (2.16)

Использование формулы Эйлера позволяет получить показательную форму комплексного числа. Именно:

z = r (cos j + i sin j) = re^ij.^.                                               (2.17)

Пример 2

Написать в показательной форме комплексные числа:

а) z = 1;   б) z = i;   в) z = 1+i;   г) z = 1–i;   д) z = –1.

Решение. а) r = 1, j = 2kp. По формуле (2.17): 2 = 2e^2kpi.

б) i = e^{i (+2kp)};    в) r = , j = +2kp, 1+i = e^{i (+2kp)};

г) 1– i = e^{i (+2kp)};    д) –1= e^{i ( p+2kp)} (k = 0, ±1, ±2, …).

Задачи для упражнений

Записать в показательной форме числа: а) ;   б) p;   в) ;   г) –i;   д) 2i;   е) 2+2i; ж). cos a + i sin a (0<a<).