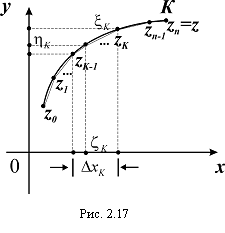
Рассмотрим в z плоскости гладкую или кусочно-гладкую кривую К с начальной z₀ и конечной z точками (рис. 2.17).

Пусть w = f(z) – функция комплексного аргумента z непрерывна на кривой К. Разобьем К произвольно на n частичных дуг точками z₀, z₁,…,z_n = z. Обозначим:  – длина вектора, т.е. длина хорды, которая стягивает дугу ; возьмем на каждой дуге по точке ; составим сумму:

,             (2.55)

которая называется интегральной. Если она имеет предел, не зависящий ни от выбора точек , и   при условии, что  при , то его называют интегралом от функции f(z) по кривой К.

Итак, по определению

.           (2.56)

Теорема: интеграл от функции f(z) по кривой К существует, если кривая-гладкая, а функция непрерывна на кривой.

Доказательство: Пусть w = f(z) = u(x,y) + iv(x,y), тогда интегральная сумма будет:

           (2.57)

Перейдя к пределу при  в (2.57), получим:

                                      (2.58)

Вывод: интеграл от функции комплексного переменного выражается через криволинейные интегралы от двух функций двух действительных переменных  u(x,y) и v(x,y).

Теорема существования криволинейных интегралов доказана в математическом анализе.

Кривая К может быть замкнутой (), и интеграл обозначается символом . При этом положительным обходом считается обход против часовой стрелки. Если кривая К задана параметрически x = x(t),  y = y(t),  ,  то

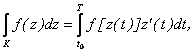                                       (2.59)

где       .

Перечислим основные свойства интеграла.

1)                                                                 (2.60)

2)      постоянная.                                                     (2.61)

3) Свойство аддитивности:

                                                                                          (2.62)

4)                                                                                                (2.63)

5)     

Эти свойства непосредственно следуют из определения интеграла (2.56).

Теорема об оценке модуля интеграла: если наибольшее значение модуля f(z) на контуре К есть число М, а длина контура интегрированная К равна l, то:

                                                            (2.64)

По определению

что и требовалось доказать.

Пример 1

Вычислить , где .

Решение. Параметрическое уравнение окружности: z(t)=Re^it, ; отсюда dz=iRe^itdt. Применяя формулу (2.59), получим:

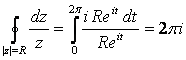.                                                (2.65)

Пример 2

Вычислить .

Решение. Уравнение окружности в этом случае имеет вид: z = a + Re^it  (), тогда

.                                           (2.66)

Пример 3

Вычислить , где , m – целое число.

Решение. Уравнение окружности |z – a| = R в параметрическом виде ; dz = Re^itidt, значит,

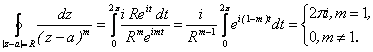
Пример 4

Вычислить , где К – ломаная с вершинами в точках О(0;0), А(1;1) и В(2;1) (сделайте рисунок).

Решение. Составим уравнение звеньев и применим свойство аддитивности: ОА: у = x или в параметрическом виде x = t,  y = t; отсюда z = x + iy = (1 + i)t ,  :

Уравнение АВ: y = 1 или x = t,  y = 1,  :

.

Итак,

Задачи для упражнений

1) Вычислить , если К:

а) прямолинейный отрезок от точки А(0;0) до В(2;1);

б) состоит из прямолинейного отрезка, соединяющего точку О(0;0) с точкой i, и прямолинейного отрезка, соединяющего точку i с точкой 2+i.

в) ломаная ОАВ: О(0;0), А(1;1), В(2;1).

Ответы: а) ;                  б) ;                     в) .

2) Вычислить 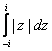, если контуром интегрирования служат:

а) прямолинейный отрезок;

б) левая половина окружности с центром О(0;0) и радиусом, равным 1;

в) правая половина той же окружности.

Ответы: а) i;              б) 2i;               в) 2i.

3) Вычислить , где К:

а) прямолинейный отрезок, соединяющий точку О(0;0) с точкой 1+3i;

б) ломаная ОАВ: О(0;0), А(1;1), В(2;1).

в) ломаная, состоящая из прямолинейного отрезка, соединяющего точку О(0;0) с точкой А(1;0), и прямолинейного отрезка от А(1;0) до точки В(1;3);

Ответы: а) ;    б) ;       в) .

4) Вычислить , если путь интегрирования есть:

а) ломаная, состоящая из отрезков, вершины которых в точках 0; 1; 1+i;

б) тоже в точках: 0; i; 1+i.

Ответы: а) ;    б)  .