Согласно теореме Коши интеграл от аналитической функции не зависит от пути интегрирования, а значит, зависит от начальной z₀ и конечной z точек кривой.

Если z₀  – фиксированная, а точка z – переменная, то

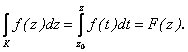                                         (2.69)

Следовательно, имеет место теорема Барроу:

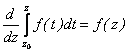,                                                 (2.70)

т.е.      F(z) – первообразная для f(z) и является аналитической, а потому имеет место формула Ньютона-Лейбница:

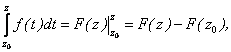                                    (2.71)

где       F(z) – одна из первообразных для   f(z).

Пример 1

Вычислить .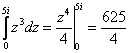

Пример 2

Вычислить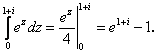

Пример 3

Вычислить и объяснить, почему  если |z| = 1, и отличен от нуля, если .

Решение. В первом случае в круге |z| < 1 подынтегральная функция – аналитическая и контур К замкнут.

Во втором случае подынтегральная функция имеет в круге |z| < 2 две особые точки, значит, может результат быть отличен от нуля.

Пример 4

Вычислить , где К: |z – (1 + i)| = 1.

Решение. Уравнение окружности |z – (1 + i)| = 1 можно записать в виде z = 1 + I + e^it,  0 £ t £ 2p В области, ограниченной этой кривой, подынтегральная функция не является аналитической, ибо в точке  1 + i  функция обращается в ¥. Поскольку dz = ie^itdt, то

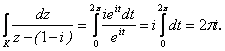
Задачи для упражнений

.