Используя основную теорему Коши, выведем формулу, которая является основной во всей ТФКП.

Теорема. Если замкнутая кривая К ограничивает односвязную область D, а функция f(z) аналитическая в ней, то для всякой внутренней точки  имеет место формула:

.                                                  (2.72)

Опишем из точки z области (рис. 2.21) как из центра, лежащую в  окружность  радиуса . В силу следствия из теоремы Коши для двусвязной области, получим:

.                                                (2.73)

В правой части (2.73) выполним тождественные преобразования:

,                           (2.74)

Согласно (2.66) , тогда

.                            (2.75)

Оценив модуль второго слагаемого в правой части равенства (2.75) (сделайте оценку самостоятельно), получили в результате нуль. Следовательно, подставляя (2.75) в (2.73), получим:

.                                                (2.76)

Эта формула называется интегральной формулой Коши.

Вывод: интегральная формула Коши позволяет находить значения аналитической функции в любой точке области D , если известны ее значения на границе К этой области.

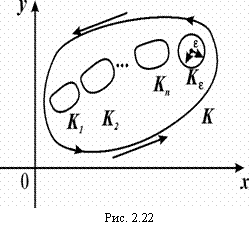
Если рассмотреть многосвязную область (рис. 2.22), границей которой служит сложный контур : К, К₁,…К_ε, Согласно теореме Коши для многосвязной области

.

Так как ,  то

.            (2.77)

Однако область, ограниченная  – односвязная, и по интегральной формуле Коши теорема доказана. На основании (2.77) получим:

.

Методическое указание

Если найти n-ю производную, дифференцируя интегральную формулу почленно по параметру z (проделайте это), можно  получить формулу:

.                                                    (2.78)

Для практических целей, переобозначая  на z, а z на z₀ формулы примут вид привычный для использования их для вычисления контурных интегралов:

                                                      (2.79)

.                                                  (2.80)

Пример 1

Вычислить: , где К:   а). |z| = 5;     б). |z| = 2.

Решение

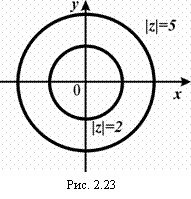а) Подынтегральная функция  аналитическая в круге |z| £ 2 (рис. 2.23), поэтому по (2.67)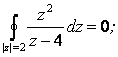

б) Воспользуемся интегральной формулой Коши (2.79), положив f(z) = z², z₀ = 4 – внутри круга. Тогда

.

Пример 2

Вычислить .

Решение. Найдя особые точки, можно записать:

.

Полагая  и z₀ = 2 видим, что f(z) – аналитическая в круге . По формуле (2.79):

.

Пример 3

Вычислить .

Решение. Положим f(z) = cos z  и  z₀ = 2i.  Тогда можно применить формулу (2.80), так как f(z) = cos z – аналитическая в круге , а точка z₀ = 2i лежит в области, ограниченной |z| = 4 (сделайте рисунок):

.

В наших условиях: ,   откуда

.

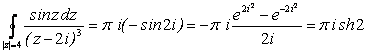Задачи для упражнений

1) Вычислить 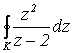, если:

а) |z| = 1;                                                            Ответ:  0;

б) |z| = 4.                                                            Ответ: .

2) Вычислить:

а) ; б) ; в) ; г) ; д) ;

е) ; ж) ; з).; и) ; к) .

Ответы:

а) ; б) ; в) ;

г) ; д)  -; е) ;

ж) ; з) 0; и) ; к) .

.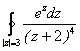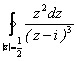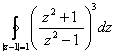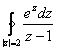