По аналогии с непрерывными системами введем в рассмотрение передаточную функцию дискретной системы , как отношение Z-изображений выходного и входного сигналов при нулевых начальных условиях:

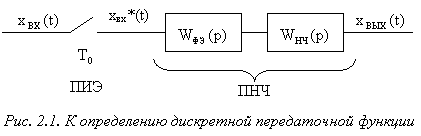
. (2.8)

В разомкнутой дискретной САУ (рис. 2.1) сигналы и – непрерывные функции времени, и формула (2.9) определяет связь не между ними, а между соответствующими решетчатыми функциями и .

Как уже отмечалось, импульсные САУ с АИМ и , являются линейными. В линейных системах, как в непрерывных, так и в дискретных, передаточная функция не зависит от вида входного сигнала. Поэтому с целью упрощения вывода формул для в качестве входного сигнала используется единичный одиночный импульс, который описывается зависимостью:

Z-изображение такого сигнала равно единице. На выходе квантователя ему будет соответствовать немодулированная -функция. Следовательно, реакция САУ на единичный одиночный импульс является функция веса ПНЧ, а ее Z-изображение совпадает с передаточной функцией :

.

Функцию веса ПНЧ можно найти, выполнив обратное преобразования Лапласа над передаточной функцией ПНЧ:

.

Таким образом, процедуру определения дискретной передаточной функции разомкнутой системы по передаточной функции ПНЧ можно условно записать в виде следующего перехода:

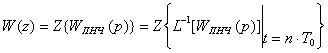. (2.9)

Пример 9

Необходимо определить , если . Для того следует выполнить преобразование выражения (2.9), начиная с вычисления непрерывной функции веса ПНЧ:

.

Соответствующая решетчатая функция веса:

.

Взяв Z-преобразование от , получим:

.

Пример 10

Необходимо определить , если передаточная функция НЧ системы имеет вид: , а в качестве ФЭ используется фиксатор с передаточной функцией (1.7).

Предварительно решим поставленную задачу в общем виде для системы с передаточной функцией НЧ . Передаточная функция ПНЧ такой системы согласно выражению (1.9) равна:

.

Следовательно,

.

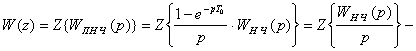
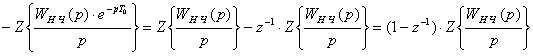В частном случае для , указанной в условии настоящего примера, имеем:

.
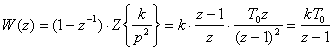