Определение 1. Особая точка z₀ называется изолированной однозначного характера, если около нее можно взять достаточно малую окрестность, что, выбросив из нее одну точку z₀, получим двусвязную область, в которой функция аналитическая.

Например, для функции 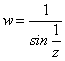 точки  – изолированные особые точки, так как в окрестности каждой из них функция аналитическая. Не то будет, если взять точку z=0. Какой бы малый радиус окрестности ни взять, в нее попадут точки разрыва  при достаточно большом k. Значит, особая точка z = 0 не будет изолированной.

Определение 2. Изолированная особая точка однозначного характера называется:

а) устранимой, если главная часть отсутствует;

б) полюсом, если главная часть содержит конечное число членов;

в) существенно особой точкой, если главная часть содержит бесконечное число слагаемых.

Порядком полюса называется число n, когда n есть низшая отрицательная степень разности z – z₀ в главной части разложения функции.

Пример 1

. Особая точка z = 0, так как

.

Следовательно, точка z = 0 – устранимая.

Пример 2

,  z = 0 – особая, так как

Следовательно, z  =0 – существенно особая точка функции.

Пример 3

,  z = 0 – особая, так как

Значит z = 0 – полюс первого порядка.