Операционное исчисление (символическое) свои истоки берет в методах символического исчисления Хевисайда. В наше время операционное исчисление считается признанным и широко применяется в различных областях науки и техники. В основе его используется преобразование Лапласа:
. (3.1)
Этот метод отличается простотой и эффективностью. Современный математический аппарат операционного исчисления позволяет решать задачи и исследовать переходные и периодические процессы в линейных и физических системах электротехники, автоматики, радиотехники, механики, описываемых системами линейных дифференциальных уравнений и уравнений с частными производными, дифференциально-разностными уравнениями, линейными дифференциальными уравнениями с переменными коэффициентами и интегральными уравнениями. Большая универсальность метода позволяет эффективно получать решения наиболее простыми и экономными путями и средствами.
Здесь будут изложены необходимые сведения из операционного исчисления, разобраны примеры и задачи для закрепления теоретического материала, касающегося дифференциальных уравнений и их систем. Для лиц, желающих углубить познания, приводится список литературы.
Преобразование Лапласа (3.1) представляет собой линейное интегральное преобразование некоторой действительной функции 
действительного переменного t в функцию 
комплексного переменного 
.
Функция 
, которая стоит под знаком интеграла в (3.1) называется оригиналом, а функция 
– ее изображением.
Оригинал должен удовлетворять условиям:
1) – однозначная, непрерывная или кусочно-непрерывная вместе со своими производными при t ³ 0;
2) 
– растет не быстрее, чем некоторая показательная функция, что означает существование постоянных, независящих от t, при которых 
;
3) 
.
Множество функций-оригиналов будем обозначать D, т.е. f(t) Î D.
Интеграл Лапласа (3.1), называемый часто прямым преобразованием Лапласа функции – несобственный. Он равномерно и абсолютно сходится, если есть оригинал. Это подтверждает теорема: для всякого оригинала изображение определено в полуплоскости 
, где 
есть показатель роста и является в этой полуплоскости аналитической функцией.
Доказательство. Оценим интеграл (3.1):
(3.2)
Для любой полуплоскости 
, интеграл, являющийся результатом дифференцирования интеграла Лапласа по p, сходится равномерно, так как он не превосходит величины, не зависящей от p:
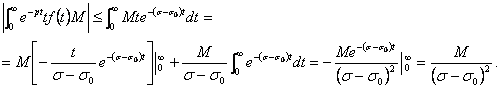
Отсюда, на основании известной теоремы [10] заключаем, что 
в полуплоскости имеет производную, следовательно, является аналитической функцией.
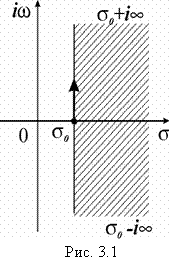В плоскости комплексного переменного 
прямая 
называется осью сходимости, а 
– абсциссой сходимости интеграла Лапласа (рис. 3.1). Интегрирование в правой части (3.1) происходит вдоль любой прямой, параллельной мнимой оси и расположенной на расстоянии 
от нее, причем все особые точки функции 
остаются слева от этой прямой.
Соответствие между изображением и оригиналом будем обозначать знаком 
и записывать так:
F(p) f(t) или f(t)
F(p).
Отметим, что острие стрелки всегда направлено к оригиналу. Условимся в дальнейшем обозначать через 
оригиналы функций, а через 
– соответствующие им изображения. Операцию получения изображения будем в необходимых случаях обозначать так: 
.
Во многих случаях бывает необходимо находить оригинал f(t) по его изображению, т.е. выполнять обратное преобразование или находить обращение преобразования Лапласа.
Формула обращения, определяющая оригинал по известному его изображению F(p) записывается в виде:
(3.3)
Эта формула называется формулой Римана-Меллина или формулой обращения преобразования Лапласа.
Замечание. Помимо изображения по Лапласу (3.1) применятся также изображение функции по Карсону:
, (3.4)
отличающееся от преобразования Лапласа множителем р. В последнее время в технической литературе все чаще пользуются изображением по Лапласу. Это объясняется наличием наглядной связи между операторным методом и гармоническим анализом, вносящей физический смысл в понятие изображения. Изображение по Лапласу 
– это спектральная функция по отношению к затухающей функции 
, для которой переменная 
является частотой [11].