Если после очередного интервала начисления доход не выплачивается, а присоединяется к денежной сумме, имеющейся на начало данного интервала, наращенную сумму определяют по формуле сложных процентов. В современный период сложные ссудные проценты являются широко распространенным видом применяемых в различных  финансовых операциях процентных ставок. В формулах, приведенных ниже, приняты следующие обозначения:

i_c – относительная величина годовой ставки сложных ссудных процентов;

k_Н.С  – коэффициент наращения при применении сложных процентов;

j –  номинальная ставка сложных ссудных процентов.

При годовом интервале начисления наращенная сумма по окончании первого года в соответствии с формулой (3.7) составит:

.                                                   (3.23)

Еще через год данное выражение применяется уже к сумме S₁:

                                            (3.24)

и так далее по каждому последующему году. Следовательно, по прошествии n лет     наращенная сумма составит:

.                                                        (3.25)

Множитель наращения k_н.с соответственно возрастет до рассчитываемой величины:

.                                                     (3.26)

При начислении простых процентов он составлял бы по формулам (3.5) и (3.7):

.                                                       (3.27)

Сравнение формул (3.26) и (3.27) для коэффициентов наращения показывает, что чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов. Поэтому при наличии выбора между низкой сложной процентной ставкой и более высокой простой следует предпочесть первый вариант.

Если срок ссуды в годах n не является целым числом, то множитель наращения определяют по выражению:

,                                               (3.28)

где n = n_a + n_b. Здесь  n_a – целое число лет; n_b – оставшаяся дробная часть года.

Если уровень ставки сложных процентов на различных интервалах начисления – разный, наращенная сумма в конце первого интервала начисляется в соответствии с формулой (3.7) и составляет:

.  

В конце второго интервала:

и далее, аналогичным образом. При N интервалах начисления наращенная сумма в конце всего периода начисления составит:

.                                                    (3.29)

Если все интервалы начисления одинаковы, что характерно для практики, и ставка сложных процентов одна и та же, формула (3.29) принимает вид

.                                                        (3.30)

Сложные проценты могут начисляться не один, а несколько раз в году. В таком случае устанавливается номинальная ставка процентов j – годовая ставка для определения величины ставок процентов на каждом интервале начисления. При m равных интервалах начисления и номинальной процентной ставке j эта величина равна j/m. При сроке ссуды n лет (аналогично формуле (3.25)) выражение для определения наращенной суммы принимает следующий вид:

,                                                   (3.31)

где mn – общее число интервалов начисления за весь срок ссуды.

Если общее число интервалов начисления не является целым числом, то выражение (3.31) принимает вид

,                                          (3.32)

где mn – целое число интервалов начисления;  l – часть интервала начисления.

Для целого числа периодов начисления следует применять формулу сложных процентов (3.25), а для дробной части – формулу простых процентов (3.7). В современный период в нашей стране наиболее распространено начисление процентов по полугодиям, по кварталам и ежемесячно. Проценты, начисляемые с определенной определенностью, называются дискретными. В мировой практике применяется непрерывное начисление сложных процентов, при котором продолжительность интервала стремится к  нулю, а их количество – к бесконечности. Для начисления наращенной суммы в таком случае применяют следующую формулу:

.                                            (3.33)

Для проведения расчетов также применяют математическую формулу

,

где e=2,71828… Из данной формулы следует:

.

Тогда формула для определения наращенной суммы принимает вид:

.                                                            (3.34)

В данной формуле

.                                                           (3.35)

Величину наращенной суммы S можно рассчитать с применением финансового калькулятора или по специальным таблицам.

Как и в случае простых процентов, полученные формулы допускают преобразо

вания путем выражения одних величин через другие, в зависимости от того, что известно и что необходимо рассчитать. Из формулы (3.25) получаем:

.                                                  (3.36)

В данной формуле коэффициент дисконтирования a является величиной, обратной коэффициенту наращения, т.е.  kн.с*а = 1. Формула (3.36) и соответствующие формулы для случая простых ставок судного процента и для учетных ставок показывают, что текущий финансовый эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок ее получения и чем выше норма доходности. Из формулы (3.25) также получаем:

.                                                    (3.37)

Из формулы (3.31) имеем:

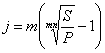.                                                  (3.38)

Применяя логарифмирование к обеим частям формулы (3.5), получаем:

.                                                     (3.39)

Аналогичным образом можно получить из формулы (3.31) формулу

.                                                   (3.40)