Метод Зейделя можно рассматривать как модификацию метода итераций для решения систем линейных уравнений, отличие состоит лишь в том, что при вычислении k-го приближения полученные  компоненты вектора  сразу же используются в вычислениях. В координатной записи итерационный процесс Зейделя имеет вид:

,

,

,

…………………………………………….

.

Начальный вектор .

В матричной записи: , где матрицы P, U получены разложением матрицы С в сумму: C = U + P.

Матрица U – верхняя треугольная часть С, включая диагональ; P – нижняя поддиагональная часть С.

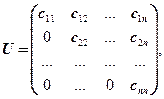
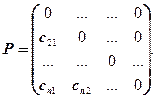
То есть .