Введем предварительные определения.  

· Рассмотрим вектор n-мерного пространства: .

Определение: Нормой вектора ||x|| называется неотрицательное действительное число, такое что

1) ||x|| = 0   тогда и только тогда, когда   x = 0;

2) ,   где a – действительное число;

3) ||x+y|| £ ||x|| + ||y||,    для любых векторов x, y.

Выделяют три нормы вектора x:

первая норма вектора                        ;

вторая норма вектора            ;

третья норма вектора             .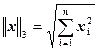

Пример 1

Пусть x = (1, -2, 3, -4).

;            ;       .

· Рассмотрим квадратную матрицу А(n ´ n) (квадратная таблица, составленная из элементов и имеющая n строк и n столбцов).

Определение: Под нормой матрицы А = [] понимается неотрицательное действительное число ||А||, удовлетворяющее следующим условиям:

1) ||А|| = 0 тогда и только тогда, когда А = 0 (А – нулевая матрица, = 0);

2) ||αА|| = |α| ||А|| , где α – действительное число;

3) ||А+В|| ||А|| + ||В|| для любых матриц А и В;

4) ||A×B||||A||×||B|| для любых матриц А и В.

Определим три нормы матрицы:

первая норма матрицы          ;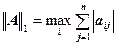

вторая норма матрицы          ;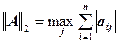

третья норма матрицы           .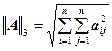

Пример 2

Пусть .

,          ,          .

Каждой квадратной матрице А соответствует определитель (детерминант) матрицы, который обозначается: det(A). Определитель  det(A) – действительное число, если элементы А – действительные числа.

Пример 3

.

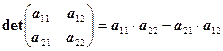Главными минорами квадратной матрицы А называют следующие n чисел:

 – первый главный минор;

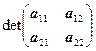 – второй главный минор;

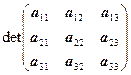 – третий главный минор;

……………………….

det(A) – n-й главный минор.

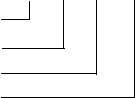
В приведенной ниже матрице отмечены первые четыре главные миноры:

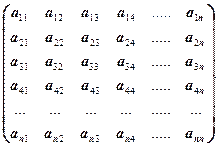
В дальнейшем мы будем рассматривать численные методы решения систем линейных уравнений. Эти методы разделяют на прямые (или точные) и итерационные (или приближенные) методы решения систем линейных уравнений.

Метод решения системы линейных уравнений называется прямым, если за конечное число арифметических действий с точными числами (то есть в отсутствие ошибок округления) можно получить точное решение системы линейных уравнений. В противном случае метод является итерационным.

Таким образом, прямые методы – это методы, погрешность которых равна нулю. Но общая погрешность этих методов при работе с действительными числами не равна нулю за счет погрешности вычислений на ЭВМ.

Итерационные методы – это методы, погрешность которых больше нуля даже в отсутствии ошибок округления.

Сначала мы рассмотрим прямые методы (метод Гаусса, метод Гаусса-Жордана), затем итерационные (метод итераций, метод Зейделя).

Рассмотрим систему линейных уравнений: Ax = b, где А – квадратная матрица n ´ n;  b – вектор правой части размерности n;   x – вектор решения размерности n;     A и b заданы, требуется определить x.

Из курса линейной алгебры известно, что для системы линейных уравнений Ax = b возможны три случая:

1) система линейных уравнений имеет единственное решение;

2) система линейных уравнений не имеет решения;

3) система линейных уравнений имеет бесконечное множество решений.

Известно, что система линейных уравнений  имеет единственное решение, если det(A)0.

Матрицы, для которых det(A)0, называются  невырожденными. В курсе линейной алгебры также изучается метод решения системы линейных уравнений с использованием вычислений определителей, называемый методом Крамера или правилом Крамера.

Рекомендуемая литература: /1-7, 9, 11, 12, 15, 16 /.