Если немодулированную последовательность - функций представить в виде комплексного ряда Фурье:

,

то выражение (1.5) для сигнала на выходе квантователя можно переписать следующим образом:

,

где  – частота квантования.

Преобразования Лапласа последнего выражения имеет вид:

.

Используя теорему L-преобразования об умножении оригинала на экспоненту, получим:

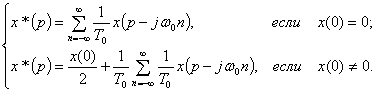                       (4.1)

Приведенные выражения означают, что L-изображения выходного сигнала квантователя являются периодическими функциями с периодом, равным , т.е.

,

где k – целое число.

Осуществив в системе (4.1) замену p на , перейдем к спектральной характеристике сигнала на выходе ПИЭ:

.

Очевидно, что спектр этого сигнала пропорционален сумме смещенных (транспортированных) спектров непрерывного сигнала на входе квантователя. Кроме того, он периодичен по частоте с периодом, равным частоте квантования , и поэтому полностью определен в полосе частот , которая называется основной полосой.

С учетом того, что спектр любого сигнала является четной функцией, симметричной относительно частоты , он может быть полностью описан в частотном диапазоне .

Таким образом, в спектре квантованного сигнала по сравнению со спектром соответствующего непрерывного сигнала присутствуют дополнительные высокочастотные составляющие. Как известно, существует однозначная зависимость между спектральной характеристикой сигнала и описывающей его функцией времени. Любое искажение спектра сигнала соответствует потере информации, которая в нем заключена.

Сформулируем условия, при которых введение в систему импульсного элемента не приводит к такой потере.

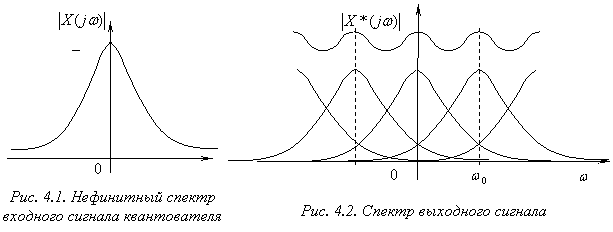
Если спектр  не ограничен по частоте (не является финитным) (рис. 4.1), то искажений избежать не удается из-за наложения высокочастотных «хвостов» смещенных спектров (рис. 4.2).

Рассмотрим случай, когда спектр  ограничен по частоте (финитен), т.е.

, если ,

где  – частота среза (рис. 4.3).

Если , также происходит наложение транспортированных спектров, в результате чего в основной полосе частот наблюдается различие между спектральными характеристиками  и  (рис. 4.4).

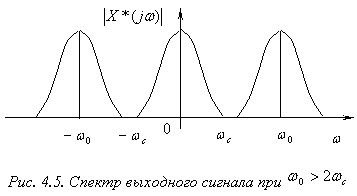
Когда , наложение смещенных спектров не происходит (рис. 4.5), и в основной полосе частот спектральные характеристики  и , совпадая по форме, различаются лишь масштабом.

Если на выходе квантователя установлен идеальный фильтр низких частот, обладающей частотной характеристикой:

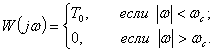                                           (4.2)

то спектр его выходного сигнала во всем частотном диапазоне будет совпадать со спектром квантуемого сигнала, т.е. на выходе такого фильтра будет восстановлен сигнал .

Следовательно, если непрерывный сигнал  обладает финитным спектром с частотой среза , то квантование по времени этого сигнала с частотой  не приводит к его искажению (теорема Котельникова-Шеннона).

Необходимо отметить следующие ограничения, связанные с применением сформулированной теоремы:

во-первых, частотная характеристика формирующего элемента, подключенного к выходу квантователя, существенно отличается от характеристики (4.2), в частности, для фиксатора в этом легко убедиться, сопоставив выражения (1.8) и (4.2);

во-вторых, не существует реальных сигналов с финитным спектром, хотя их высокочастотные составляющие могут быть сильно ослабленными.