Многие электроизоляционные материалы в той или иной степени гигроскопичны, т.е. способны сорбировать влагу из окружающей среды, и влагопроницаемы, т.е. способны пропускать влагу.

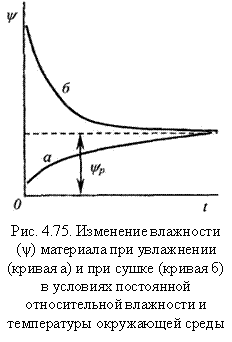
Гигроскопичность. Образец электроизоляционного материала при определенных условиях влажности и температуры окружающей среды через некоторое время достигает некоторого «равновесного» состояния влажности. Так, если сравнительно сухой образец материала находится во влажном воздухе с относительной влажностью φ, то будет наблюдаться постепенное поглощение материалом влаги из воздуха. Причем влажность материала (ψ), т.е. содержание влаги на единицу массы материала, в течение времени t будет повышаться, асимптотически приближаясь к равновесному значению ψ_p, соответствующему значению ψ (рис. 4.75, кривая а). Наоборот, если при тех же условиях образец из такого же материала обладает высокой начальной влажностью, то влажность образца будет уменьшаться, асимптотически приближаясь к равновесной ψ_p; в этом случае происходит сушка материала (рис.4.75, кривая б).

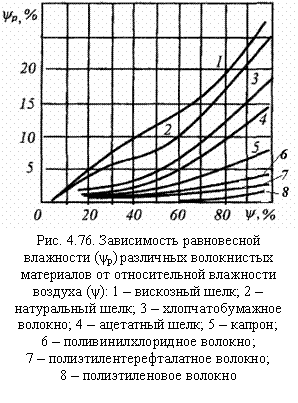
Для различных материалов значения равновесной влажности при одном и том же значении относительной влажности воздуха могут значительно различаться (рис. 4.76).

При повышении температуры равновесная влажность, соответствующая тому же значению ψ_p, понижается. Таким образом, сушке способствуют кроме пониженной влажности окружающей среды и смены воздуха (вентиляции), обусловливающей соприкосновение с поверхностью материала новых объемов сухого воздуха, повышение температуры.

Под гигроскопичностью (в узком смысле слова) или влагопоглощаемостъю подразумевают равновесную влажность данного материала при нормальной температуре в воздухе, относительная влажность (ψ_p) которого близка к 100 %.

Иногда электроизоляционные материалы соприкасаются не только с воздухом, содержащим пары воды, но и непосредственно с водой. Такова изоляция открытых установок, подвергающихся действию атмосферных осадков, изоляция электрических машин и аппаратов на кораблях, в насосах и т.п. В таких случаях представляет интерес водопоглощаемость изоляции.

Материалы анизотропного строения впитывают влагу в разных направлениях с различной скоростью. Так, дерево скорее впитывает влагу вдоль волокон, т.е. с торцевого спила ствола; слоистые пластики – вдоль слоев и т.д.

Гигроскопичность материала зависит от его строения. Большую роль играют наличие и размер капиллярных пор внутри материала, в которые проникает влага. Сильно пористые материалы, в частности волокнистые, более гигроскопичны, чем материалы плотного, сплошного строения. Гигроскопичность материалов, практически лишенных пор (например, стекол), может быть только поверхностной: поглощаемая из окружающей среды влага накапливается в виде тонкой пленки на поверхности материала, но не проникает вглубь.

Гигроскопичность и водопоглощаемость не полностью отражают степень возможных изменений электрических свойств электроизоляционного материала при увлажнении. Если поглощенная влага способна образовывать внутри изоляции нити или пленки, которые могут пронизывать весь промежуток между электродами (или значительную область этого промежутка), то даже весьма малые количества поглощенной влаги приводят к очень резкому ухудшению электрических свойств изоляции. Если же влага распределяется по объему электроизоляционного материала в виде отдельных, не соединенных между собой малых включений, то влияние влаги на электрические свойства материала менее существенно. Так, например, удельное сопротивление бумаги с 3%-й влажностью приблизительно в 10⁶ раз меньше, чем абсолютно сухой бумаги, в то время, как увлажнение каучуковых материалов с наполнителями вызывает лишь весьма незначительное уменьшение их ρ. Для несмачиваемых материалов уменьшение  при выдержке во влажной среде незначительно, так как влага даже в виде росы образует отдельные капли, а не сплошную водяную пленку.

Влагопроницаемость. Кроме гигроскопичности большое практическое значение имеет влагопроницаемость материалов, т.е. способность их пропускать через себя пары воды. Это свойство очень важно при оценке качества материалов, применяемых в виде защитных покровов (для шлангов кабелей, компаундных заливок, лаковых покрытий изоляции электрических машин и т.п.). О возможности проникновения влаги через мельчайшие поры можно судить по размеру молекулы воды, диаметр которой составляет 2,5·10^{-10 м.}

Коэффициент влагопроницаемости (П) электроизоляционного материала входит в основное уравнение влагопроницаемости. Количество воды (М), проходящее при стационарном режиме за время t сквозь участок площадью S слоя рассматриваемого материала толщиной h, если с двух сторон пленки существуют парциальные давления водяного пара в воздухе  и  соответственно, равно:

.                                            (4.140)

Это уравнение формально аналогично закону Ома при прохождении через тело электрического тока (причем разность давлений  подобна разности потенциалов, отношение  – току, a  – электрическому сопротивлению тела) или уравнению теплопроводности.

Из уравнения (4.140) получается единица СИ для измерения П:

кг/(м·с·Па) = 1с.

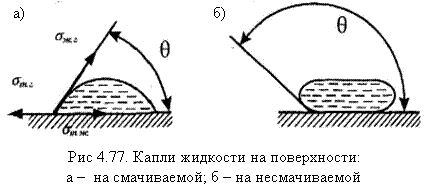
Способность твердого тела смачиваться водой (или другой жидкостью), характеризуется краевым углом смачивания (θ) капли воды, нанесенной на поверхность тела (рис. 4.77). Чем меньше θ, тем сильнее выражена смачиваемость материала. Для смачиваемых поверхностей θ < 90° (рис. 4.77, а), для несмачиваемых θ > 90° (рис. 4.77, б).

Для уменьшения гигроскопичности и влагопроницаемости пористых электроизоляционных материалов широко применяют их пропитку.

Значение равновесного краевого угла определяется соотношением сил притяжения жидкости к твердому телу (адгезией), и сил взаимного притяжения между частицами самой жидкости (сила когезией). Соотношение между работой адгезии и когезии определяет способность жидкости смачивать поверхность твердого тела.

Поверхностное натяжение – это сила, действующая по касательной к поверхности жидкости. Поверхностное натяжение стремится сократить свободную поверхность жидкости до минимальных размеров. Сила поверхностного натяжения численно равна удельной свободной поверхностной энергии.

Удельная свободная поверхностная энергия измеряется в тех же единицах, что и поверхностное натяжение (эрг/см²; Дж/м²).

По периметру смачивания твердого тела каплей жидкости действуют три поверхностных натяжения на границах раздела:

· твердое тело – газ (σ_т.г.);

· жидкость – газ (σ_ж.г.);

· жидкость – твердое тело (σ_ж.т.).

Поверхностное натяжение, на границе раздела «твердое тело – газ» увеличивает площадь соприкосновения жидкости с твердой поверхностью и способствует растеканию капли. В противоположность этому поверхностное натяжение σ_ж.т. препятствует растеканию капли и стремится сохранить границу раздела «жидкость – твердое тело». Поверхностное натяжение на границе жидкости с газом (σ_ж.г) стремится уменьшить поверхность капли. Оно направлено под углом θ к твердому телу.

В условиях равновесия капли можно записать:

,                                                   (4.141)

где  – энергия смачивания. С помощью этого уравнения можно оценивать адгезию жидкости к поверхности твердого тела.

Энергия смачивания, энергия поверхностного натяжения и краевой угол смачивания определяются методом погружения. Этот метод основан на измерении веса пластины при погружении ее в жидкость. При этом происходит втягивание или выталкивание твердого тела в зависимости от того, смачивается или не смачивается оно жидкостью. Метод погружения пластины применяют для краевых углов на гидрофильных твердых телах. При соприкосновении такого тела с поверхностью жидкости будет происходить втягивание его в жидкость, что приведет к кажущемуся увеличению веса пластины на величину Δm.

Выталкивающая сила будет противодействовать увеличению веса пластины и для момента равновесия можно записать:

,                                      (4.142)

где  – энергия смачивания, кг/с² (кг/с² = Дж/м² = 10⁷эрг/м²); ρ – плотность жидкости, кг/м²; S – поперечное сечение пластины, м²; h – глубина погружения пластины в жидкость, м; g – ускорение силы тяжести (м/с²); Δm – разность в весе сухой и частично погруженной в жидкость пластины, кг;  – периметр пластины, м.

Глубина погружения пластины складывается из двух составляющих: глубины втягивания пластины жидкостью () и высоты подъема жидкости в сосуде, вследствие вытеснения ее пластиной (). Поэтому можно записать:

.

       (4.143)

Высота подъема жидкости в сосуде зависит от площади ее поверхности () и поперечного сечения пластины (S):

.              (4.144)

Так как поперечное сечение пластины много меньше площади поверхности жидкости в сосуде (), следовательно, и , тогда уравнение (4.143) можно упростить:

.

 (4.145)

Слагаемое  в формуле (4.145) представляет архимедову силу и по абсолютному значению много меньше Δm. Слагаемое ; при небольших (до 5 мм) глубинах погружения пластинки  . С учетом этого уравнение (4.143) принимает вид:

.        (4.146)

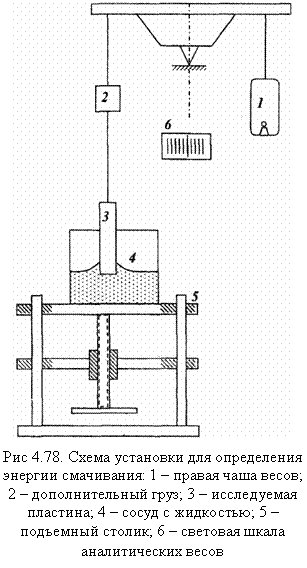
Энергию смачивания измеряют на  специальной  установке (рис. 4.78). На аналитических весах 6 определяют вес исследуемой пластинки твердого тела. Затем, сняв левую чашку весов, вместо нее подвешивают пластинку и уравновешивают весы с помощью дополнительного груза 2, примерно равного по весу снятой чашке весов. Под свободный конец висящей пластины 3 подводят подъемный столик 5 со стоящим на нем сосудом с жидкостью 4. Поднимая, сосуд с помощью подъемного столика 5, доводят до соприкосновения поверхности жидкости с концом пластины 3. Момент соприкосновения регистрируется по резкому отклонению «зайчика» на световой шкале весов 6. Вследствие смачивания пластинки жидкостью она погружается в нее на некоторую глубину h.

Разница в значениях веса пластинки после втягивания ее в жидкость () и до соприкосновения с поверхностью (m) жидкости численно равна увеличению ее веса на  Δm:

.                                                 (4.147)

Используя уравнение (4.146), рассчитывают энергию смачивания (адгезионное напряжение):

.

Для определения угла смачивания жидкости используют метод отрыва пластины. Медленно опуская сосуд с жидкостью, регистрируют значение веса пластины в момент отрыва ее от поверхности жидкости, при этом наблюдается резкий скачок светового «зайчика» на шкале весов 6 (рис. 4.78). Обозначив увеличение веса пластинки в момент отрыва через , получим:

.                                                                    (4.148)

Затем рассчитываем значение угла смачивания:

,                                                 (4.149)