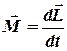Моментом импульса материальной точки относительно неподвижной точки (![]() ) называется физическая величина, определяемая векторным произведением:
) называется физическая величина, определяемая векторным произведением:
![]() ,
,
 где
где ![]() -радиус-вектор, проведенный из точки О в точку А;
-радиус-вектор, проведенный из точки О в точку А; ![]() - импульс материальной точки (рис. 4.4);
- импульс материальной точки (рис. 4.4); ![]() – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
– псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от ![]() к
к ![]() .
.
Модуль вектора момента импульса равен:
![]()
где ![]() – угол между векторами
– угол между векторами ![]() и
и ![]() ;
; ![]() – плечо вектора
– плечо вектора ![]() относительно точки O.
относительно точки O.
Моментом импульса относительно неподвижной оси (z) называется скалярная величина (![]() ), равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки (О) данной оси. Момент импульса (
), равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки (О) данной оси. Момент импульса (![]() ) не зависит от положения точки О на оси z.
) не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса ![]() с некоторой скоростью
с некоторой скоростью ![]() . Скорость
. Скорость ![]() и импульс
и импульс ![]() перпендикулярны этому радиусу, то есть радиус является плечом вектора
перпендикулярны этому радиусу, то есть радиус является плечом вектора ![]() . Поэтому можем записать, что момент импульса отдельной частицы равен:
. Поэтому можем записать, что момент импульса отдельной частицы равен: ![]() и направлен по оси в сторону, определяемую правилом правого винта.
и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
![]() . (4.1)
. (4.1)
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцировав уравнение (4.1) по времени получим:
![]() , то есть
, то есть ![]() .
.
Это выражение есть еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Физический смысл этого выражения: скорость изменения момента импульса равна моменту сил.
В векторной форме это можно записать так:
 ;
;
В замкнутой системе момент (![]() ) внешних сил равен нулю и, следовательно,
) внешних сил равен нулю и, следовательно, 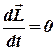 , откуда
, откуда
![]() = сonst. (4.2)
= сonst. (4.2)
Выражение (4.2) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы не изменяется с течением времени. Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, то есть с инвариантностью физических законов относительно выбора направления осей координат системы отсчета. Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение:
|
Поступательное движение |
Вращательное движение |
||||
|
Масса |
|
Момент инерции |
|
||
|
Скорость |
|
Угловая скорость |
|
||
|
Ускорение |
|
Угловое ускорение |
|
||
|
Сила |
|
Момент силы |
|
||
|
Импульс |
|
Момент импульса |
|
||
|
Основные уравнения динамики |
|
Основные уравнения динамики |
|
||
|
Работа |
|
Работа |
|
||
|
Кинетическая энергия |
|
Кинетическая энергия |
|
||
|
Закон сохранения импульса |
|
Закон сохранения момента импульса |
|
||