Рассмотрим неограниченную струну ![]() . Уравнение свободных колебаний однородной струны имеет вид
. Уравнение свободных колебаний однородной струны имеет вид
![]() . (4.28)
. (4.28)
Положим
![]() (4.29)
(4.29)
Видно, что x – at = C1, x + at = C2 – есть характеристики уравнения (4.28). Это уравнение в новых переменных запишется в виде:
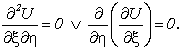
Из последнего имеем:
![]()
где ![]() – произвольная функция
– произвольная функция ![]() . Интегрируя это уравнение по
. Интегрируя это уравнение по ![]() , найдем:
, найдем:
![]()
где ![]() – произвольная функция от
– произвольная функция от ![]() . Положим
. Положим
![]() ,
,
получим:
![]() .
.
Возвращаясь к старым переменным х и t, будем иметь:
![]() . (4.30)
. (4.30)
Решение (4.30) уравнения (4.28) называется решением Даламбера (методом характеристик).
Пусть требуется найти решение уравнения (4.28), удовлетворяющее начальным условиям:
![]() . (4.31)
. (4.31)
Ввиду того, что струна бесконечная функции ![]() и
и ![]() заданы в
заданы в ![]() . В решении (4.30) нашего уравнения нужно выбрать функции
. В решении (4.30) нашего уравнения нужно выбрать функции ![]() и
и ![]() так, чтобы удовлетворить начальным условиям (I.4.4). Из начальных условий (4.31) имеем
так, чтобы удовлетворить начальным условиям (I.4.4). Из начальных условий (4.31) имеем
![]() ,
,
откуда, интегрируя второе равенство, получим
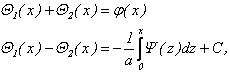 (I.4.5)
(I.4.5)
где С – произвольная постоянная.
Из равенства (4.32) найдем:
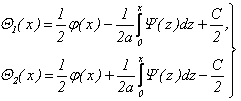 (4.33)
(4.33)
Подставим (4.33) в (4.30), получим:
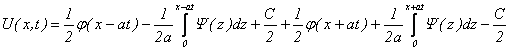
или окончательно
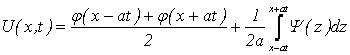 . (4.34)
. (4.34)
Формула (4.34) даёт решения задачи Коши, если ![]() имеет непрерывные производные до второго порядка включительно, а
имеет непрерывные производные до второго порядка включительно, а ![]() – до первого. Задача Коши поставлена корректно, а решение её единственное. Это видно из вывода формулы Даламбера.
– до первого. Задача Коши поставлена корректно, а решение её единственное. Это видно из вывода формулы Даламбера.
Пример 1
Найти решение уравнения: ![]() , если
, если ![]() .
.
Решение. Граничные условия отсутствуют, следовательно, струна – бесконечна в обе стороны. По формуле Даламбера:
![]() .
.
По условию задачи: ![]() поэтому
поэтому
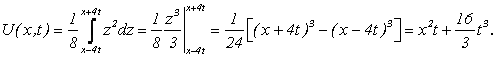
Пример 2
Найти форму струны, описываемую уравнением: ![]() в момент
в момент ![]() , если
, если
![]()
Решение. Здесь ![]() . Следовательно, по (4.34) получим
. Следовательно, по (4.34) получим
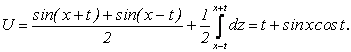
Если ![]() , то
, то ![]() – струна параллельна оси Ох.
– струна параллельна оси Ох.
Пример 3
Найти решение уравнения: ![]() , если
, если ![]()
![]()
Решение. По формуле Даламбера ![]()
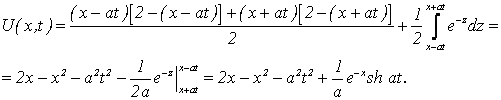
Ответ: ![]()