Формально метод модифицированного Z-преобразования основан на определении Z-изображения модифицированного сигнала , т.е. сигнала , задержанного фиктивным звеном чистого запаздывания на время .

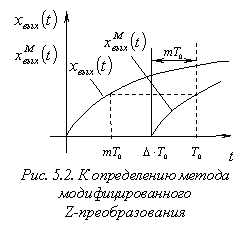
Рассмотрим подробнее один, например первый, интервал квантования (рис. 5.2). Поскольку

,

очевидно, что, изменяя  от 1 до 0, можно по величине дискреты  определить все значения  от  до .

Для удобства дальнейших преобразований введем в рассмотрение величину , диапазон изменения которой от 0 до 1.

Z-изображение модифицированного сигнала:

 

.                      (5.2)

При  

и, следовательно, функция  задержана на один такт по сравнению с .

При  

,

т.е. модифицированное и «обычное» Z-изображения совпадают.

Пример 25

Необходимо определить модифицированное изображение линейно нарастающего сигнала .

В соответствии с выражением (5.2) получим:

.

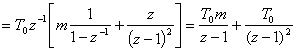При

.

Модифицированное Z-изображение выходного сигнала разомкнутой системы (см. рис. 2.1) с передаточной функцией ПНЧ  определим следующим образом:

.                                             (5.3)

Здесь  – модифицированная дискретная передаточная функция, для вычисления которой необходимо выполнить модифицированное Z-преобразование функции веса, соответствующей :

.                                               (5.4)

При последовательном соединении звеньев дискретной САУ (см. рис. 2.2, а) модифицированное Z-изображение ее выходного сигнала равно:

а в случае, когда звенья   и  не разделены квантователем (см. рис. 2.2, б):

В замкнутой дискретной системе с квантованием сигнала ошибки (см. рис. 2.5) модифицированное Z-изображение выходного сигнала равно:

,

но

,

следовательно,

и

 

А модифицированная дискретная передаточная функция замкнутой системы равна:

                                               (5.5)

Пример 26

Необходимо определить решетчатые переходные функции  и  для дискретной системы, рассмотренной в примере 22.

Передаточная функция системы равна:

Для определения  воспользуемся формулой (2.20). Полагаем:

 

Тогда:

Значения дискрет:

                     и т.д.

Модифицированные дискретные передаточные функции разомкнутой и замкнутой систем равны соответственно:

 

и

где ,

Здесь важно отметить тот факт, что для любой дискретной системы характеристические полиномы у  и  совпадают, а следовательно, совпадают и полю

са указанных передаточных функций, поэтому устойчивость САУ можно оценивать как по , так и по .

Более того, выражение для  может быть определено по :

Модифицированное Z-изображение переходной функции:

=.

Раздельно для каждого из двух слагаемых  по формуле (2.20) необходимо определить составляющие . При этом полагаем , так как они не зависят от n.

После преобразований получаем выражение для , по которому величину переходной функции можно рассчитать для произвольных моментов времени :

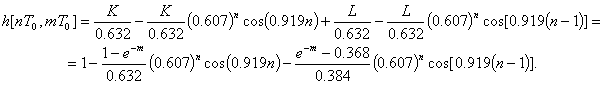
Например:

при  и ;           ;

при  и          .