Совокупность G двух множеств: А – множества вершин и С – множества дуг, называется графом. Т.е. G = (А, С).

А – множество объектов произвольной природы, С – множество формализованных связей между ними.

Геометрически вершины графа обозначаются: , а связи между ними – линиями, соединяющими вершины.

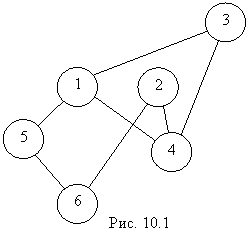Так как физические свойства объектов множества А нас интересовать не будут, то вершины будем обозначать числами. Связи или дуги будем обозначать линиями. Если существует дуга, соединяющая вершины i и j, то эти вершины называются связанными, в противном случае, несвязанными.

Довольно часто графы представляются в виде матрицы смежности вершин, в которой элементы с номерами i и j, соответствующие связанным вершинам, отмечаются единицей (1) или точкой (·), а соответствующие несвязанным вершинам – нулем (0)

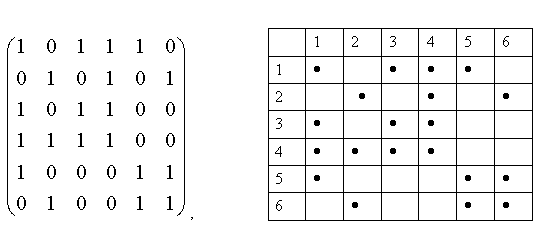или просто оставляется пустая клетка. Для графа (рис 10.1) матицы смежности вершин будут иметь вид:

Часто в матрице смежности вершинам проставляются значения, которые характеризуют дуги. Например, если C_ij – расстояние между вершинами, то матрица смежности превращается в матрицу расстояний. Если C_ij – пропускная способность дуги, то C будет называться матрицей пропускных способностей. Если C_ij – стоимость перевозки единицы груза из i в j, то С – матрица стоимостей.

Непрерывная последовательность связанных вершин называется цепью. Цепь, в которой начальные и конечные вершины совпадают, называется циклом.

Если любые две вершины графа можно соединить цепью, то он называется связанным, в противном случае – несвязанным. Связанный граф без циклов называется деревом-остовом или просто деревом.

Если существует связь между вершиной i и вершиной j, но нет обратной связи, то соответствующая дуга, соединяющая эти вершины, называется ориентированной. Поэтому граф, в котором все дуги ориентированы, называется ориентированным. В нём геометрически дуги изображаются стрелками (рис. 10.2).