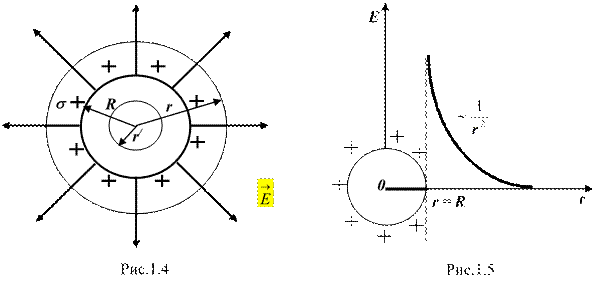
Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +s.  Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 1.4).

Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле. Тогда по теореме Гаусса (1.1), учитывая, что площадь сферы равна: , получим: . Отсюда:

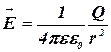  (r  ³ R),

где R – радиус сферической поверхности; Q – общий заряд; r – радиус сферы, имеющий общий центр с заряженной сферой; e – диэлектрическая проницаемость среды; e₀ – электрическая постоянная.

При r > R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости от r приведен на рис.1.5.  Если r^/ < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри заряженной сферической поверхности электростатическое поле отсутствует ( = 0).